Investigating Solids with Face-transitivity

If you have access to a set of equilateral triangles which fit together, such as Polydron, you may wish to make some of the models discussed while reading this article. If you have not met the Platonic and Archimedean solids before, start by reading the article Classifying Solids using Angle Deficiency, which provided the inspiration for Edward's ideas discussed here.

Having read the NRICH article Classifying Solids using Angle Deficiency, I wondered what would happen if, instead of relaxing the requirement that all the faces be the same (which leads to the Archimedean solids), I relaxed the requirement that all the vertices be the same. I also removed the requirement that the solids be convex.

I constructed solids which consisted of identical, regular faces where the number of faces meeting at a vertex was a characteristic of that vertex, and each face had to have the same pattern of 'vertex numbers' around its vertices.

For example, the first shape I constructed had triangular faces, with three faces meeting at one vertex and six faces meeting at the other two vertices of each triangle.
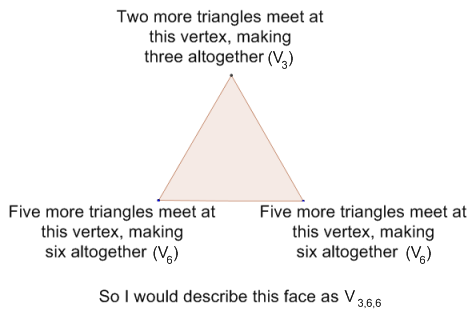
I assembled the triangles in such a way that the pattern for every face was $V_{3,6,6}$.
This resulted in a peculiar shape with 12 faces, 18 edges, and 8 vertices. It looked like four tetrahedra stuck to the faces of a fifth.

The $V_6$ vertices of the solid were not flat, as might be expected because six equilateral triangles can meet at a point to form a tessellation of the plane. Instead they folded around the vertex. The solid is concave and cannot rest on any face; only two edges at a time may rest on a plane.

I worked out the total angle deficiency which is $720^\circ$, because there are four $V_3$ vertices each with a deficiency of $180^\circ$, and four $V_6$ vertices which have zero angle deficiency.

From my analysis of the model I made, I think it has the same set of symmetries as the tetrahedron, being essentially a tetrahedron with each face replaced by another tetrahedron.

I then produced two more shapes with triangular faces, which I described as $V_{5,4,4}$ and $V_{3,4,4}$. Both of these consisted of two identical pyramids joined at their bases (pentagonal pyramids and tetrahedra respectively), and were convex. These were not so interesting as the first shape I made.


I then tried some other configurations, such as $V_{3,5,5}$ and quickly found that, for triangular faces, if you have an odd vertex number and the other two numbers are not equal to each other, the solid cannot be constructed. If I start with 5 triangles meeting at a point so that each has a $V_5$ vertex, this creates a pentagon. As each face already has one $V_5$ vertex, the remaining two vertices on each face must be one $V_3$ and one $V_5$, so around the pentagon I must alternate between $V_3$ and $V_5$ vertices. But as 5 is an odd number I cannot match the pattern when I get back to the beginning - I am forced to have either two $V_3$ or two $V_5$ vertices together. The same argument can apply to any odd vertex number, as alternating around an n-gon when n is odd will always result in two adjacent vertices needing to be the same.

I noticed that any configuration of the form $V_{a,4,4}$ for $a$< 6 will, if constructable, produce a pair of joined pyramids (see $V_{5,4,4}$ above). If $a$=4 this will, in fact, be an octahedron. However, the case $a$=6 cannot be constructed since this would produce two flat hexagons in the same plane. I don't think values of $a$ above 6 can work either, but I'm not sure.

I then tried to construct $V_{4,6,6}$. This produced a shape with 24 faces, 36 edges, and 14 vertices. It consists of a cube with each face replaced by a square pyramid; it is another concave figure, which seems to have the same symmetries as the cube from which it is formed. The angle deficiency comes from the six $V_4$ vertices (as the $V_6$ vertices have zero angle deficiency), each being deficient by $120^\circ$, so the total angle deficiency is $6\times 120^\circ = 720^\circ$.



I attempted also to construct $V_{5,6,6}$; this should have produced a figure formed from a dodecahedron with faces replaced by pentagonal pyramids, but I found it very difficult to physically construct. It might be easier to produce a computer model.

After further thought, it occurred to me that it was possible to replace the faces of any Platonic solid with pyramids, which meant that figures based on the octahedron and icosahedron could also be constructed. These would have configurations of $V_{3,8,8}$ and $V_{3,10,10}$ respectively, and would in each case share the symmetries of their 'parent' solid. Constructing $V_{3,8,8}$ produced the Stellated Octahedron (also called the Stella Octangula).


I believe that the vertex number configuration uniquely specifies the solid, so if you are given $V_{a,b,c}$ and lots of triangles, there is at most one solid you can make for a given set of values $a,b$ and $c$. I also think that the rule that all faces should have the same pattern of vertices around them is sufficient to ensure 'face-transitivity', by which I mean any face can be mapped onto any other by some symmetry of the solid. The Platonic solids are the convex solids which satisfy this rule as well as the rule for the Archimedean solids that all vertices should have the same pattern of faces around them.

One way to think about the face-transitive property is this: imagine a planet in the shape of one of the face-transitive polyhedra shown above, and imagine that you are given one of the faces as a piece of land to farm. Because the polyhedron is face-transitive, it makes no difference which face you are given, because they are all identical. Also, you cannot work out from the 'geography' of the planet where on its surface you are, since all faces are the same.

Having created solids by replacing the faces of Platonic solids with pyramids, I attempted to construct a solid from one of the Archimedean solids in the same way. I found that for each type of face on the original solid, there is a type of face on the new solid. For example, if we take the cuboctahedron and replace its triangular faces with tetrahedra and its square faces with square pyramids (using equilateral triangles), the faces which produce the tetrahedra will be $V_{3,8,8}$ and the faces which produce the square pyramids will be $V_{4,8,8}$, so it breaks my rule about every face having the same vertex numbers around it, so is not one of my face-transitive solids. However, the shape retains the symmetry of the cuboctahedron.



I began to investigate the solids formed from other regular faces besides triangles. I tried to construct $V_{3,3,3,4,4}$ from pentagons, and found that it produces an infinite tunnel of dodecahedra:



There is no obvious upper limit on the polygons that can be used, nor on how large the vertex numbers may become, since a nonconvex vertex may have a negative angle deficiency.

Edward is about to embark on a degree in Mathematics at the University of Cambridge.