Several students considered this problem with NRICH as a group. Whilst most thought initially to use algebra, they soon realised that there was no unique solution. So, the problem reduced to finding ranges of possible solutions.This was approached with a mixture of algebra and numerical methods.

Steve thought:

Before attempting any calculations I tried to make sense of the numbers, as suggested in the problem.

The first measurement point was $10$ days. Samples of cobalt $60, 57, 56, 58$ would not decay very much in this time.

Since the sample loses about one third of its mass in this time, a large component must be cobalt $58$. However, since there is still about half the sample remaining after $360$ days there must be at most about half of cobalt-58.

I worked out after 10, 90 and 360 days what fraction of a lump of sample of each pure isotope would remain. So , after 10 days about 99.6% of cobalt 60 and 0.63% of cobalt 55 would remain; after 360 days 87.8% of a mass of cobalt-60 would remain but 6.98E-80 of cobalt-55 would remain. Since this felt experimental, I made a spreadsheet where I could work out the total mass remaining for given starting sample


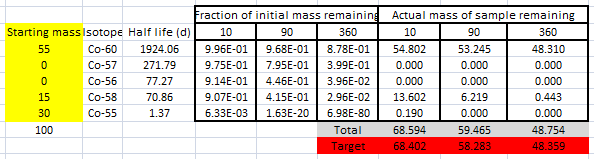
Using common sense (that Co-60 decays very slowly and Co-55 very quickly) I quickly found this solution, which matched the target masses very closely.

There are obviously other solutions, but experimentation indicated that there had to be 30g of Co-55 to match the data.

Tom thought:

Since there are only 4 conditions given (initial mass followed by three observations) and five possible isotope masses the system is under-determined, so there will be no unique solution. Looking at the data, the half lives of Co-56 and Co-58 are similar, so I will make the simplifying assumption that the masses of these two isotopes are equal.

If I choose the initial masses to be $A$, $B$, $C$, $C$, $D$ then my four equations will be

$$
\begin{eqnarray}
A+B+C+C+D &=& 100\cr
A2^{-10/1924.06}+B2^{-10/271.79}+C2^{-10/77.27}+C2^{-10/70.86}+D2^{-10/1.37}&=&68.402\cr
A2^{-90/1924.06}+B2^{-90/271.79}+C2^{-90/77.27}+C2^{-90/70.86}+D2^{-90/1.37}&=&68.402\cr
A2^{-360/1924.06}+B2^{-360/271.79}+C2^{-360/77.27}+C2^{-360/70.86}+D2^{-360/1.37}&=&68.402
\end{eqnarray}
$$
I chose to work with the numbers to 4 decimal places, as this seemed about right given the accuracies in the problem (since the masses remaining were given to 3 dp and the half lives also only to a couple of places)

This gave me equations

$$
\begin{eqnarray}
A&+&B&+&2C&+&D &=& 100\cr
0.9964A&+&0.9748B&+&1.8210C&+&0.0063D&=&68.402\cr
0.9681A&+&0.7949B&+&0.8607C&&&=&58.283\cr
0.8784A&+&0.3993B&+&0.0691C&&&=&48.359
\end{eqnarray}
$$
These looked quite intimidating to solve, but then I just got down to it and it only took a few minutes using a spreadsheet to do the algebra.

I found that $A=41.91, B=15.57,C= 6.18, D=30.14$

I then wondered about the other solutions. I found these solutions:

Isotope	Mass	Mass	Mass	Mass
Co-60	52.16	42.31	41.49	41.91
Co-57	0	15.49	15.67	15.58
Co-56	12.90	0	12.68	6.18
Co-58	4.90	12.077	0	6.18
Co-55	30.03	30.121	30.15	30.13

From this table it seems reasonable to assert that

1) There are $30$ grams of Co-55.
2) The combined mass of Co-56 and Co-58 is between 12 and 18 grams.
3) There is at most 16 grams of Co-57
4) There is at least 41 g of Co-60.