Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cobalt Decay
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Several students considered this problem with NRICH as a group. Whilst most thought initially to use algebra, they soon realised that there was no unique solution. So, the problem reduced to finding ranges of possible solutions.This was approached with a mixture of algebra and numerical methods.
Steve thought:
Before attempting any calculations I tried to make sense of the numbers, as suggested in the problem.
The first measurement point was $10$ days. Samples of cobalt $60, 57, 56, 58$ would not decay very much in this time.
Since the sample loses about one third of its mass in this time, a large component must be cobalt $58$. However, since there is still about half the sample remaining after $360$ days there must be at most about half of cobalt-58.
I worked out after 10, 90 and 360 days what fraction of a lump of sample of each pure isotope would remain. So , after 10 days about 99.6% of cobalt 60 and 0.63% of cobalt 55 would remain; after 360 days 87.8% of a mass of cobalt-60 would remain but 6.98E-80 of cobalt-55 would remain. Since this felt experimental, I made a spreadsheet where I could work out the total mass remaining for given starting sample
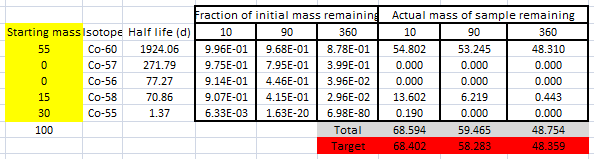
Using common sense (that Co-60 decays very slowly and Co-55 very quickly) I quickly found this solution, which matched the target masses very closely.
There are obviously other solutions, but experimentation indicated that there had to be 30g of Co-55 to match the data.
Tom thought:
Since there are only 4 conditions given (initial mass followed by three observations) and five possible isotope masses the system is under-determined, so there will be no unique solution. Looking at the data, the half lives of Co-56 and Co-58 are similar, so I will make the simplifying assumption that the masses of these two isotopes are equal.
If I choose the initial masses to be $A$, $B$, $C$, $C$, $D$ then my four equations will be
$$
\begin{eqnarray}
A+B+C+C+D &=& 100\cr
A2^{-10/1924.06}+B2^{-10/271.79}+C2^{-10/77.27}+C2^{-10/70.86}+D2^{-10/1.37}&=&68.402\cr
A2^{-90/1924.06}+B2^{-90/271.79}+C2^{-90/77.27}+C2^{-90/70.86}+D2^{-90/1.37}&=&68.402\cr
A2^{-360/1924.06}+B2^{-360/271.79}+C2^{-360/77.27}+C2^{-360/70.86}+D2^{-360/1.37}&=&68.402
\end{eqnarray}
$$
I chose to work with the numbers to 4 decimal places, as this seemed about right given the accuracies in the problem (since the masses remaining were given to 3 dp and the half lives also only to a couple of places)
This gave me equations
$$
\begin{eqnarray}
A&+&B&+&2C&+&D &=& 100\cr
0.9964A&+&0.9748B&+&1.8210C&+&0.0063D&=&68.402\cr
0.9681A&+&0.7949B&+&0.8607C&&&=&58.283\cr
0.8784A&+&0.3993B&+&0.0691C&&&=&48.359
\end{eqnarray}
$$
These looked quite intimidating to solve, but then I just got down to it and it only took a few minutes using a spreadsheet to do the algebra.
I found that $A=41.91, B=15.57,C= 6.18, D=30.14$
I then wondered about the other solutions. I found these solutions:
| Isotope | Mass | Mass | Mass | Mass |
| Co-60 | 52.16 | 42.31 | 41.49 | 41.91 |
| Co-57 | 0 | 15.49 | 15.67 | 15.58 |
| Co-56 | 12.90 | 0 | 12.68 | 6.18 |
| Co-58 | 4.90 | 12.077 | 0 | 6.18 |
| Co-55 | 30.03 | 30.121 | 30.15 | 30.13 |
From this table it seems reasonable to assert that
1) There are $30$ grams of Co-55.
2) The combined mass of Co-56 and Co-58 is between 12 and 18 grams.
3) There is at most 16 grams of Co-57
4) There is at least 41 g of Co-60.