Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Bicentric Quadrilaterals
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We
received a great solution from Zhi of St. Marylebone CE School. She
begins with a diagram:
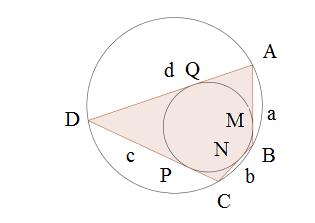
In the diagram presented, the vertices of the quadrilateral are labeled A, B, C and D, and tangent points M, N, P and Q respectively. The sides are labelled a, b, c and d.
From the properties of the circles we know that the tangents AM and AQ, BM and BN, CN and CP, DP and DQ are equal respectively. Therefore, if the quadrilateral is to be tangential, AQ+DQ+BN+CN would have to be equal to AM+DP+BM+CP, which then becomes:
$$AD+BC=AB+CD$$ Therefore, we know that a tangential quadrilateral has to satisfy AD+BC=AB+CD.
Using the properties of isosceles triangles and angle bisectors, we can deduce that the reverse is also true, meaning that all quadrilaterals satisfying $AD+BC=AB+CD$ are tangential. Is the reverse obvious? The question only asks for a necessary condition so in fact we do no need to show the reverse but this could be a nice extension.
The properties of cyclic quadrilaterals imply that for any cyclic quadrilateral ABCD, $\angle A+\angle C = \angle B +\angle D = 180^{\circ}$.The reverse is also true. Can you show this condition is necessary? See the problem Circles in Quadrilaterals.

In the diagram presented, the vertices of the quadrilateral are labeled A, B, C and D, and tangent points M, N, P and Q respectively. The sides are labelled a, b, c and d.
From the properties of the circles we know that the tangents AM and AQ, BM and BN, CN and CP, DP and DQ are equal respectively. Therefore, if the quadrilateral is to be tangential, AQ+DQ+BN+CN would have to be equal to AM+DP+BM+CP, which then becomes:
$$AD+BC=AB+CD$$ Therefore, we know that a tangential quadrilateral has to satisfy AD+BC=AB+CD.
Using the properties of isosceles triangles and angle bisectors, we can deduce that the reverse is also true, meaning that all quadrilaterals satisfying $AD+BC=AB+CD$ are tangential. Is the reverse obvious? The question only asks for a necessary condition so in fact we do no need to show the reverse but this could be a nice extension.
The properties of cyclic quadrilaterals imply that for any cyclic quadrilateral ABCD, $\angle A+\angle C = \angle B +\angle D = 180^{\circ}$.The reverse is also true. Can you show this condition is necessary? See the problem Circles in Quadrilaterals.
Therefore, a bicentric
quadrilateral ABCD has to meet two conditions
- $AD+BD=AB+CD$ and
- $\angle A + \angle C = \angle B +\angle D = 180 ^{\circ}$
With that , we can now
deduce:
- Squares are always bicentric
- Rectangles and rhombi, provided that they aren't squares, cannot be bicentric as rectangles do not satisfy condition 1, and rhombi do not satisfy condtion 2.
- Irregular parallelograms do not meet either condition and cannot be bicentric
- Trapezia might or might not be bicentric, depending on their side lengths and angles.
Zhi then went on to prove the formula for the
area of a bicentric quadrilateral. We shall omit the proof here
since the question only asks you to verify that the formula works
on the examples you found. If you are interested see the proof of
brahmagupta's formula and try to adapt it to this
problem.