Bicentric Quadrilaterals

Stage: 4 Challenge Level: Challenge Level:3 Challenge Level:3 Challenge Level:3

First, try the problem Circles in Quadrilaterals to familiarise yourself with the properties of tangential quadrilaterals.

A bicentric quadrilateral is both tangential and cyclic. In other words, it is possible to draw a circle inside it which touches all four sides, and also to draw another circle around it which passes through all four vertices. (The two circles do not necessarily have the same centre!)


Here is a picture of a bicentric quadrilateral.
Example of a bicentric quadrilateral
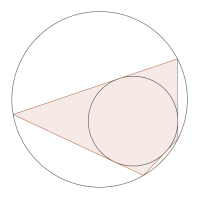
Think about special quadrilaterals, such as squares, trapezia, and parallelograms.
  • Which types of quadrilateral are always bicentric?
  • Which types of quadrilateral are never bicentric?
  • For the quadrilaterals which are sometimes bicentric, can you explain the conditions necessary for them to be bicentric?

There is a formula for finding the area $A$ of a bicentric quadrilateral:
$$ A = \sqrt{abcd} $$

where $a,b,c$ and $d$ are the lengths of the four sides.

Verify that this formula gives the correct area for the examples of bicentric quadrilaterals you have found.

search engine page

Published September 2009.