 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Round and Round



- Problem
- Student Solutions
- Teachers' Resources
Well done Kang Hong Joo from the Chinese High School, Singapore; Lucinda Hearth from Stamford High School; Jessica Zhang; Matthew Hodgetts from King Edward VI Camp Hill School, Birmingham; Tom Davie and Michael Grey from Madras College, St. Andrews.
Case 1: a semicircle

Let the radius of the inner circle be $r$; then its area is $\pi{r^2}$. The area of the semicircle is $\pi(2r)^2/2$, which is $2\pi{r^2}$. The percentage of the semicircle covered by the inner circle is 50\%.
Case 2: a quadrant 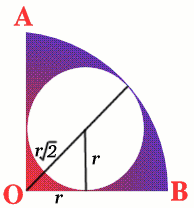
The area of the inner circle is $\pi{r^2}$; the radius of the
quadrant is $r(1 + \sqrt{2})$, and the area of the quadrant is
$$\frac{1}{4}\pi{r^2}(1 + \sqrt{2})^2 = \frac{1}{4}\pi{r^2}(3 +
2\sqrt{2})$$ Therefore $$\frac{\text{area of inner
circle}}{\text{area of quadrant}} = \frac{4}{3 + \sqrt{2}} =
68.6\%$$
Case 3: a sector of angle
$2\alpha$
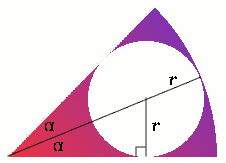
The area of the inner circle is $\pi{r^2}$. Taking the radius of the sector to be 1 unit, then $$\sin\alpha = \frac{r}{1 - r}$$ Hence $$r = \frac{\sin\alpha}{1 + \sin\alpha}$$ The area of the sector is ${1\over2} 1^2 (2a) = a$ or, equivalently, ${\pi{\alpha}\over180}$ if $\alpha$ is measured in degrees.
Therefore $$\frac{\text{area of inner circle}}{\text{area of sector}} = \frac{\pi\sin^{2}\alpha}{\alpha(1 + \sin\alpha)^2}$$ When $\alpha = {\pi\over6} = 30^{\circ}$, then $\sin\alpha = {1\over2}$, and this ratio is $2/3$.
When $\alpha = {\pi\over3} = 60^{\circ}$, then $\sin\alpha = {\sqrt{3}\over2}$, and this ratio is $$\frac{3\pi/4}{(\pi/3)(1+\sqrt{3}/2)^2} = \frac{9}{2+\sqrt{3}} = 9(2 - \sqrt{3})^2 = 64.6 \%$$
| a | 30 o | 45 o | 60 o | 90 o |
| Ratio (nearest 1%) |
67% | 69% | 65% | 50% |