Round and round
Problem
Prove that the shaded area of the semicircle is equal to the area of the inner circle.

What percentage of the sector OAB is taken up with the inner circle?
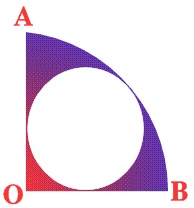
What happens if angle AOB is less than 90 ° or between 90 and 180 degrees?
Student Solutions
Well done Kang Hong Joo from the Chinese High School, Singapore; Lucinda Hearth from Stamford High School; Jessica Zhang; Matthew Hodgetts from King Edward VI Camp Hill School, Birmingham; Tom Davie and Michael Grey from Madras College, St. Andrews.
Case 1: a semicircle

Let the radius of the inner circle be $r$; then its area is $\pi{r^2}$. The area of the semicircle is $\pi(2r)^2/2$, which is $2\pi{r^2}$. The percentage of the semicircle covered by the inner circle is 50\%.
Case 2: a quadrant 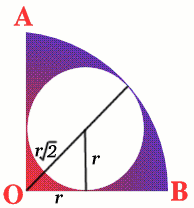
The area of the inner circle is $\pi{r^2}$; the radius of the
quadrant is $r(1 + \sqrt{2})$, and the area of the quadrant is
$$\frac{1}{4}\pi{r^2}(1 + \sqrt{2})^2 = \frac{1}{4}\pi{r^2}(3 +
2\sqrt{2})$$ Therefore $$\frac{\text{area of inner
circle}}{\text{area of quadrant}} = \frac{4}{3 + \sqrt{2}} =
68.6\%$$
Case 3: a sector of angle
$2\alpha$
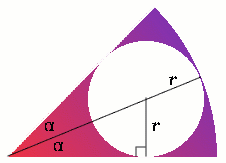
The area of the inner circle is $\pi{r^2}$. Taking the radius of the sector to be 1 unit, then $$\sin\alpha = \frac{r}{1 - r}$$ Hence $$r = \frac{\sin\alpha}{1 + \sin\alpha}$$ The area of the sector is ${1\over2} 1^2 (2a) = a$ or, equivalently, ${\pi{\alpha}\over180}$ if $\alpha$ is measured in degrees.
Therefore $$\frac{\text{area of inner circle}}{\text{area of sector}} = \frac{\pi\sin^{2}\alpha}{\alpha(1 + \sin\alpha)^2}$$ When $\alpha = {\pi\over6} = 30^{\circ}$, then $\sin\alpha = {1\over2}$, and this ratio is $2/3$.
When $\alpha = {\pi\over3} = 60^{\circ}$, then $\sin\alpha = {\sqrt{3}\over2}$, and this ratio is $$\frac{3\pi/4}{(\pi/3)(1+\sqrt{3}/2)^2} = \frac{9}{2+\sqrt{3}} = 9(2 - \sqrt{3})^2 = 64.6 \%$$
| a | 30 o | 45 o | 60 o | 90 o |
| Ratio (nearest 1%) |
67% | 69% | 65% | 50% |
