Dan, Rohin, Sam and Sam from Grindon Hall Christian School sent in this solution:

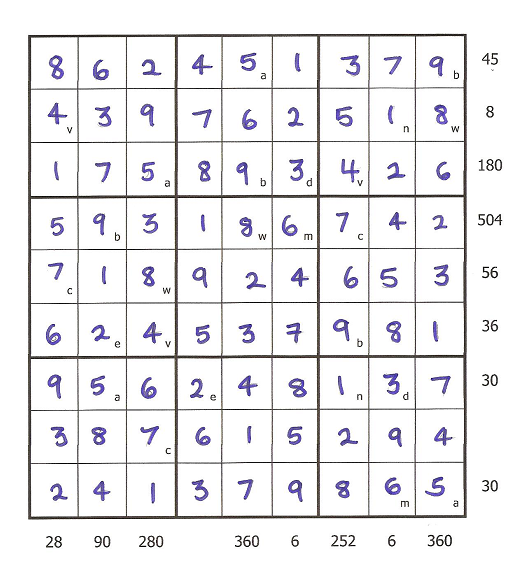
First we worked out the letters in the left hand column which were v and c. We worked out that it could only be 7 and 4 because they were the only two numbers that were below 10 that had an LCM of 28. We saw that c=7 and v=4 because v was on a row where it had to be a multiple of 8.

Next, we worked out the middle row. We did this by using the 7 that we got earlier, and worked out that the only number that would give an LCM of 56 would be 8, so w=8. We then filled in the v, c and w squares.

Next, we worked out that a and b were 9 and 5 - because they are the only numbers from 1-9 to give an LCM of 45. We worked out that b had to be 9 because 5 does not go into 36 (6th row). So a=5 and b=9 and we filled in all the a and b squares. On the bottom row we needed an LCM of 30. We already knew a=5, so that meant that m had to be 6.

Next, we worked out that e=2 by looking at the second column. We already had the 9 and the 5 and we needed an LCM of 90 - 2 was the only number that worked in this situation from the ones we had left. In the seventh column we needed an LCM of 252 and we already had 9, 7 and 4 which have an LCM of 252, so the missing variable had to be 1, so n=1. We then filled in the e and n squares. After that the only remaining letter was d and the only number we had left was 3, so d=3. That worked because the LCM of 5,2,1 and 3 gave us 30 on the seventh row.

The resulting grid was a regular Sudoku, and we filled the numbers in using the normal rules.
 

Rhea from Loughborough High School solved this problem in a different way:

First, I started by looking for two rows or columns which had at least one letter in common. I started with ones which only had 2 letters:
a and b = LCM 45 (top row)
a and m = LCM 30 (bottom row)
The only two numbers between 1 and 9 which have an LCM of 45 are 5 and 9. Likewise, the only two numbers which have an LCM of 30 are 5 and 6. As 5 is the common number and a is the common letter, I knew that: 
a = 5, and I deduced from this that b = 9 and m = 6.
I filled in these numbers and looked for rows and columns which had the letters a,b or m as well as other numbers:
a,b and e = LCM 90 (second row from the left)
I can calculate that e has to be 2, because if it was 1,3 or 9- the LCM of the three numbers whould be 45. I filled in all the e's in the sudoku grid and then looked at the second row from the right:
n,d and m = LCM 6
We know that m = 6 and e = 2; the only remaining factors of 6 are 3 and 1 so-
n/d = 3/1 i.e. I didn't yet know which letter was which number.
After this, I looked at the row which had 56 as its LCM (the very middle row) and had two letters- c and w. I knew that these letters must be 7 and 8 because they are the only numbers between 1 and 9 which have an LCM of 56. The letter c also lies in the first column on the left, which has an LCM of 28. As 7 is a multiple of 28 and 56 and 8 isn't, I could conclude that:
w = 8
c = 7 From this I could also conclude that:
v = 4 (in the first column), as the LCM of 4 and 7 is 28.
After these figures were filled in, I was left with two numbers- 1 and 3, and two letters- n and d. When I looked at the second row to the top, where 4, 8 and n had an LCM of 8, I concluded that n = 1 and d = 3 because 8 is not a multiple of 3 but is a multiple of 1.
I know that I got all the numbers right because I was able to fill in the sudoku.

And here is a link to that sudoku.