LCM Sudoku
Here is a Sudoku with a difference! Use information about lowest common multiples to help you solve it.
Problem
LCM Sudoku printable worksheet

Rules of LCM Sudoku
- Each column, each row and each 3x3 box must have the numbers 1 to 9.
- No column, row or box can contain the same number more than once.
- The nine letters in the grid each represent a different number from 1 to 9.
- The numbers at the end of the rows and at the bottom of the columns are the Lowest Common Multiples (LCM) of the letters in that row.
- The LCM of the variables b, w, m and c in the fourth row is 504.
- As an example, the LCM of 8, 9, 6, 4, 2, 5 and 7 is 2520.
Here is the complete route she took through the lettered cells:
Charlie worked out the value of the letters in the following order: a, m, b, w, c, v, e, n, d
Here is the complete route he took through the lettered cells:
Steve worked out the value of the letters in the following order: c, v, w, a, b, m, e, n, d
Here is the complete route he took through the lettered cells:
Can you work out the values of the nine letters in the same order that they did?
Can you work out the values of the letters in any other orders?
After finding the values of all the variables, you can solve the rest of the Sudoku using standard techniques and strategies.
After completing this Sudoku you may like to have a go at LCM Sudoku II
Thank you to Henry Kwok for devising this Sudoku.
Getting Started
You can express $8, 9, 6, 4, 2, 5$ and $7$ as $2^3, 3^2, 2 \times 3, 2^2, 2, 5$ and $7$.
That means the LCM must contain $2^3, 3^2, 5$ and $7$ to ensure that it is a multiple of all the numbers.
So the LCM is $2^3 \times 3^2 \times 5 \times 7 = 2520$.
Student Solutions
Dan, Rohin, Sam and Sam from Grindon Hall Christian School sent in this solution:
First we worked out the letters in the left hand column which were v and c. We worked out that it could only be 7 and 4 because they were the only two numbers that were below 10 that had an LCM of 28. We saw that c=7 and v=4 because v was on a row where it had to be a multiple of 8.
Next, we worked out the middle row. We did this by using the 7 that we got earlier, and worked out that the only number that would give an LCM of 56 would be 8, so w=8. We then filled in the v, c and w squares.
Next, we worked out that a and b were 9 and 5 - because they are the only numbers from 1-9 to give an LCM of 45. We worked out that b had to be 9 because 5 does not go into 36 (6th row). So a=5 and b=9 and we filled in all the a and b squares. On the bottom row we needed an LCM of 30. We already knew a=5, so that meant that m had to be 6.
Next, we worked out that e=2 by looking at the second column. We already had the 9 and the 5 and we needed an LCM of 90 - 2 was the only number that worked in this situation from the ones we had left. In the seventh column we needed an LCM of 252 and we already had 9, 7 and 4 which have an LCM of 252, so the missing variable had to be 1, so n=1. We then filled in the e and n squares. After that the only remaining letter was d and the only number we had left was 3, so d=3. That worked because the LCM of 5,2,1 and 3 gave us 30 on the seventh row.
The resulting grid was a regular Sudoku, and we filled the numbers in using the normal rules.
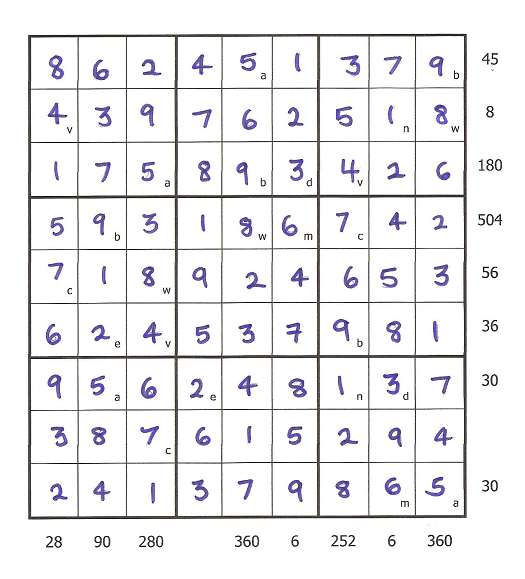
Rhea from Loughborough High School solved this problem in a different way:
First, I started by looking for two rows or columns which had at least one letter in common. I started with ones which only had 2 letters:
a and b = LCM 45 (top row)
a and m = LCM 30 (bottom row)
The only two numbers between 1 and 9 which have an LCM of 45 are 5 and 9. Likewise, the only two numbers which have an LCM of 30 are 5 and 6. As 5 is the common number and a is the common letter, I knew that:
a = 5, and I deduced from this that b = 9 and m = 6.
I filled in these numbers and looked for rows and columns which had the letters a,b or m as well as other numbers:
a,b and e = LCM 90 (second row from the left)
I can calculate that e has to be 2, because if it was 1,3 or 9- the LCM of the three numbers whould be 45. I filled in all the e's in the sudoku grid and then looked at the second row from the right:
n,d and m = LCM 6
We know that m = 6 and e = 2; the only remaining factors of 6 are 3 and 1 so-
n/d = 3/1 i.e. I didn't yet know which letter was which number.
After this, I looked at the row which had 56 as its LCM (the very middle row) and had two letters- c and w. I knew that these letters must be 7 and 8 because they are the only numbers between 1 and 9 which have an LCM of 56. The letter c also lies in the first column on the left, which has an LCM of 28. As 7 is a multiple of 28 and 56 and 8 isn't, I could conclude that:
w = 8
c = 7 From this I could also conclude that:
v = 4 (in the first column), as the LCM of 4 and 7 is 28.
After these figures were filled in, I was left with two numbers- 1 and 3, and two letters- n and d. When I looked at the second row to the top, where 4, 8 and n had an LCM of 8, I concluded that n = 1 and d = 3 because 8 is not a multiple of 3 but is a multiple of 1.
I know that I got all the numbers right because I was able to fill in the sudoku.
And here is a link to that sudoku.
Teachers' Resources
Why do this problem?
This problem provides an engaging and challenging context in which to practise working with Lowest Common Multiples.
Possible approach
Show the grid below, or hand out this worksheet.

"Here is a Sudoku with a difference. As usual:
Each column, each row and each 3x3 box must have the numbers 1 to 9.
No column, row or box can contain the same number more than once.
The nine letters in the grid each represent a different number from 1 to 9."
"What makes this different is that:
The numbers at the end of the rows and at the bottom of the columns are the Lowest Common Multiples (LCM) of the letters in that row.
The LCM of the variables b, w, m and c in the fourth row is 504."
If necessary, recap with students how to work out LCMs.
"This is a really interesting problem because it can be solved in lots of different ways. Alison, Charlie and Steve worked on this problem. I am going to hand out a record of their work, showing the order in which they worked out the value of the letters. Your challenge is to work out the values of the nine letters in the same order that they did."
Towards the end, bring the class together to compare the merits of different routes.
Key questions
How many different combinations of three numbers have a LCM of 12?
$180$ appears on row three, and its prime factorisation is $2^2 \times 3^2 \times 5$. What can you deduce for certain about the letters on that row?
Possible support
Students could work in pairs to make sense of the different routes.
Possible extension
"Can you work out the values of the letters in any other orders?"
