 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
The Patent Solution



- Problem
- Student Solutions
Copyright © Kenneth Kelsey
The following puzzle comes from The Ultimate Book of Number Puzzles
by Kenneth Kelsey and David King, published by The Cresset Press
1992. Sadly this book, which contains 350 intriguing puzzles to
solve, is now out of print; you might just be lucky enough to find
it on a second hand bookstall.
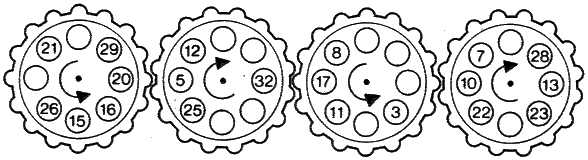 .
.
"Your late father was, as you know, a rather eccentric inventor," said the solicitor to Peter, "and he has bequeathed to you the patent specification relating to the combination mechanism for safes. It comprises thirty-two tumblers numbered from one to thirty-two. When the combination is first set these tumblers have to be inserted into four cog wheels in such a way that the numbers in each wheel total 132."
"There's nothing patentable in that, surely?" asked Peter.
"No, but in addition every horizontal row of eight tumblers must also total 132..."
"Nor in that."
"... and continue to do so even when the cog wheels are turned."
"Good heavens! Is that possible?"
"It must be since the patent has been incorporated into several safes. Unfortunately when your father filed the patent application he deliberately omitted several of the numbers from the specification drawings in order to keep the relative positions of the tumblers a trade secret. He kept the completed drawings locked away in his private safe together with all his securities."
"Well then," said Peter "let's look in there."
"That's the problem," said the solicitor. "We can't open the darned thing until we have the combination!"
From the incomplete specification given in the diagram shown above, could you open the safe? In solving this puzzle bear in mind that there are 16 positions for each cog wheel, not eight as one might initially believe. The constant of 132 is obtained from the three horizontal lines of eight tumblers in all 16 positions as well as from the sum of the eight tumblers in each cog wheel.