Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
The Patent Solution
Age 11 to 14
Challenge Level 





- Problem
- Student Solutions
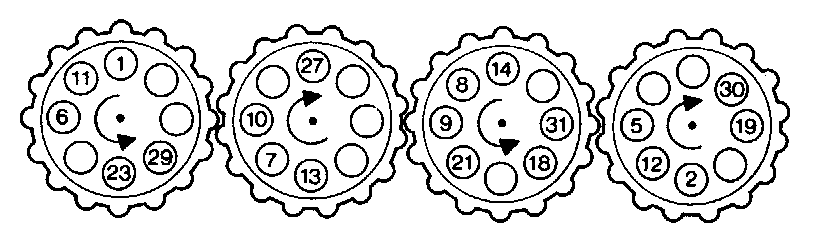
This is quite a challenge and it is really a magic square in disguise! Here is one solution and another similar puzzle for you to try. You may like to study the articles Magic Squares and Magic Squares II.
Patent Solution solution
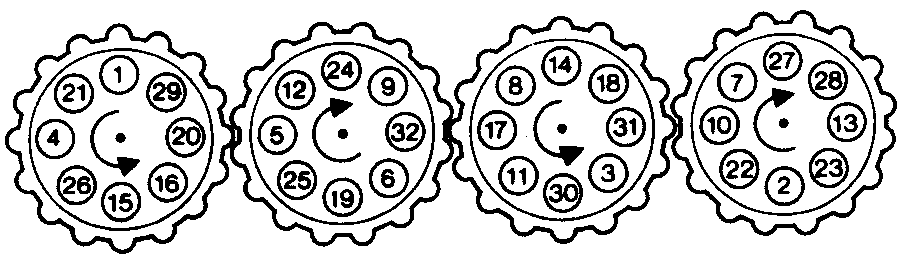
Another Patent Puzzle - again the magic total is 132
The following puzzle comes from The Ultimate Book of Number Puzzles by Kenneth Kelsey published by The Cresset Press 1992, ISBN: 0 09 177204 4.