Developing a framework for mathematical enrichment
Abstract
"In mathematics the ability to solve problems is not just
knowing some straightforward rules"
Polya
(1957)
The NRICH Project (www.nrich.maths.org) has been in operation
since 1996. Since this time the resources on the web site have
grown and the project has developed a reputation for creative
thinking in the area of mathematics enrichment.
The most recent work of the project has centred on making more
effective use of the wealth of resources we now have available to
us, both in terms of access to the enormous archive and in creating
meaningful frameworks within which selections of the material can
be placed (enrichment trails). As the new site and trails have
developed we have questioned our understanding of mathematics
enrichment and how it might be represented in classroom practice
and through the NRICH site itself. The reflection and early
research findings have resulted in two key outcomes that are having
a fundamental impact on our work:
- the resources have something to offer pupils of nearly all abilities. This has resulted in the structuring of the site and creation of the trails to facilitate a "free flow" of resources across age and ability boundaries.
- enrichment is not only an issue of content but a teaching approach that offers opportunities for exploration, discovery and communication,
- effective mediation offers a key with which to unlock the barriers to engagement and learning.
We are attempting to address the issues of the nature of
enrichment, accessibility, mediation and the philosophies of
learning and teaching that underpin our work both through the
structure and content of the site, our work on enrichment trails
and our face to face work with pupils and teachers.
This paper considers the key aspects of mathematics enrichment
and how the content and design of trails (as well as the NRICH site
itself) has been influenced by, and built upon, these
philosophies.
Background and Rationale
The wider context
The United Kingdom Numeracy Framework offers guidance and
exemplification of the mathematics curriculum giving content,
structure and guidance on its implementation and delivery. However,
although there has been an overall improvement in performance in
national tests, there are areas where concerns still exist in terms
of performance, teaching and attitudes to mathematics:
- Concerns exist over pupil performance in algebra, geometry and problem solving (Brown, Millett et al. 2000). These concerns have most recently resulted in changes to the national mathematics attainment tests, which will now include a problem solving section.
- Most commonly, the needs of most able pupils are met through courses of acceleration. Pupils undertaking such courses are often taught independently (and separately) from their peers, older pupils often having to go to other schools for their lessons. These models of acceleration pose medium to long term problems of sustainability and there is no evidence of long-term benefits. Ability grouping with "fast track" top sets has also been shown to cause problems in the long term (Boaler, Wiliam et al. 2000).
- Fewer pupils are choosing to study mathematics and mathematics related subjects beyond the age of 16 (Nardi and Steward 2002), (Nardi and Steward 2002) (Nardi and Stewart 2003 forthcoming).
- Evidence of lack of motivation and consequent dips in performance across KS3 is available and indicates pupils are being "turned off" mathematics. (Watson, 2001). Results in 2003 show a slight decline in performance over previous years resulting in the government adjusting long term performance targets.
Enrichment can be used:
- to support the most able alongside all children in the class; often offering differentiation by outcome,
- to promote mathematical reasoning and thinking skills, preparing pupils through breadth and experience to tackle higher level mathematics with confidence and a sense of pattern and place.
Mathematics Enrichment Materials on the NRICH Website
There have been a wealth of resources that support
mathematical enrichment, most notably the NRICH online mathematics
project (www.nrich.maths.org). The resources on the NRICH site have
been in "loose leaf" format; being stored with few pointers to
their curriculum context and relevance. This has left the user with
issues of access to appropriate material and knowledge of the
potential of, and means by which, the material can be used to
support the development of high level mathematical reasoning (and
other) skills.
From these points come the foci of our recent work:
- identification of key aspects of an enrichment curriculum for mathematics that makes links between content, the national frameworks, and practice explicit;
- effective presentation and structuring of resources on the NRICH site such that they will underpin an enrichment framework by offering exemplars of content and supporting material.
It is through examining the theories underpinning the
development of structured content (trails) and views of teachers as
users of the trails, the nature of mathematical enrichment and how
it can be represented is being implemented.
Defining a Framework
Terms such as "mathematical thinking", "mathematical problem
solving" and "enrichment" are variously described in current
literature. Our work has therefore involved us in clarifying
definitions of these terms. Establishing meanings has involved a
literature review, interviews with colleagues and teachers and the
analysis of NRICH team discussions. In addition, the process of
site and trail development has involved multiple iterations which
have themselves informed the definitions. These definitions are
therefore constantly being reviewed and refined as we trial and
test materials and build the framework within which our work is
set. What is presented is our current view of these terms as they
relate to our work.
Enrichment
In current literature, "enrichment" is almost exclusively used
in the context of provision for the mathematically most able.
However, there is strong evidence from the use of the NRICH site,
and our own experience working with teachers and pupils, that this
fails to address the value of an enrichment approach to teaching
mathematics generally. Problems which offer suitable entry points
can be used with pupils of a wide range of ability and therefore
can be used within the "ordinary" classroom. The teacher or mentor
can use such materials in flexible ways that respond to the needs
(and experience) of the learner. We see enrichment as an approach
to teaching and learning mathematics that is appropriate for all
not simply the most able. NRICH resources therefore continue to
support the most able but this is within the context of a broad
interpretation and view of enrichment not within a context of
provision simply targeting the most able. Good enrichment education
is good education for all. Good mathematics education should
incorporate an approach that is an enriching and stimulating
experience for all pupils. The construction of enrichment we are
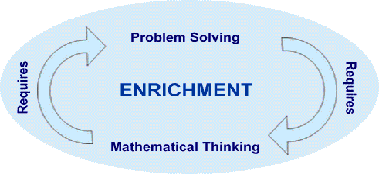
adopting thus builds on two main threads:
Content
This thread describes an enrichment curriculum, which has the
following components:
- Content opportunities designed to:
-
- develop and use problem solving strategies,*
- encourage mathematical thinking,*
- include historical cultural contexts,
- offer opportunities for mathematical extension.
* These two strands form the focus of the content discussion
in this paper
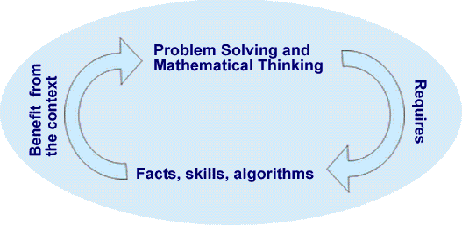
Enrichment is not simply learning facts and demonstrating
skills. Mathematical skills and knowledge can be a precursors to,
and also outcomes of, an enrichment curriculum (needs driven
learning). The aim of an enrichment curriculum is to support:
- a problem solving approach
- improving pupil attitudes
- a growing appreciation of mathematics
- the development of conceptual structures
based on Ernest (2000)
Enrichment therefore represents an open and flexible approach
to teaching mathematics which encourages experimentation and
communication.
Image
Teaching approach
This places an emphasis on teaching that reflects a
constructivist view of learning and which stresses:
- non-assertive mediation,
- group work, discussion, communicating...,
- varied solutions and different approaches being valued and utilised,
- exploration, making mathematical connections, extending boundaries, celebrating ideas not simply answers, flexibility...,
- acknowledgment that maths is hard but success is all the more enjoyable when a hurdle is overcome.
Problem Solving and Mathematical Thinking
A range of literature exists in the areas of Problem solving
and Mathematical thinking, the two terms often being used
synonymously or with a lack of clarity in their inter-relationship.
As part of our framework for development we have been able to
identify two distinct threads that appear in the use of the two
terms and which are worthy of articulation and distinction. These
threads pull together ideas drawn from current theory (Mayer
(2002); Koshy (2001); Mason, Burton and Stacey (1985); Ernest
(2000), Shoenfeld (1994), Polya (1957), Lester (1994), Cobb et al
(1991), Van Zoest et al (1994), and our own work in the
field.
We are taking "mathematical thinking" to mean particular
mathematical strategies that are employed in solving problems of
different types. Some exemplars of these strategies are given
below. The aim is to identify problems where such strategies are
useful and create a curriculum thread that encourages pupils to
develop each strategy and identify the type of context and the ways
is which such strategies can be employed.
Problem solving is reserved for the structural approach to
solving problems - the overview, or steps on the journey from
meeting a problem for the first time to its solution. Problem
solving identifies and developments competence in utilising the
stages on the route through solving a problem. Problem solving
underpins the vast majority of NRICHs resources.
Thus mathematical thinking strategies are needed to tackle
problems and will be used within the problem solving process.
Mathematical Thinking Strategies:
Some of the mathematical thinking strategies we have
identified include:
- Conjecturing/theorising;
- Being systematic;*
- Identifying common structures (isomorphisms);*
- Introducing variables;
- Generalising;*
- Specialising/clarifying/looking for specific examples;
- Considering a special case (the particular);
- Solving simpler related problems;
- Reflecting on experience - have you met something like this before?
- Multiple representations;
- Working backwards;
- Identifying and describing patterns;
- Representing information - diagram, table
- Testing ideas - guessing and testing (hypothesizing).
*We have begun to develop curriculum resources that illustrate
and support these aspects of mathematical thinking, in the form of
trails.
There is still some work to do in identifying different
aspects of mathematical thinking .Not all these strategies have a
similar feel to them. Currently it seems easier to implement a
developmental schema for some than for others.
Problem Solving Process
There are a number of descriptions of what constitutes problem
solving within the literature (Mason et al (1985), Mayer (2002),
Ernest (2000), Polya (1957)). These references have many common
threads and have models of the process that are broken down into a
varied number of stages. The process outlined below combines a
number of the features of these existing models with our own
research findings.
The C.A.P.E. model
- Comprehension
-
- Making sense of the problem/retelling/creating a mental image,
- Applying a model to the problem;
- Analysis and synthesis
-
- Identifying and accessing required pre-requisite knowledge,
- Applying facts and skills, including those listed in mathematical thinking (above),
- Conjecturing and hypothesising (what if);
- Planning and execution
-
- Considering novel approaches and/or solutions
- Identifying possible mathematical knowledge and skills gaps that may need addressing,
- Planning the solution/mental or diagrammatic model,
- Execute;
- Evaluation
-
- Reflection and review of the solution,
- Self assessment about ones own learning and mathematical tools employed,
- Communicating results.
Despite its representation, this is not a simple linear model
-sometimes it is necessary to revisit and review several times -one
can think of the problem solving process as a spiralling inward
towards a satisfactory conclusion.
Image
Implications for teaching for enrichment
I have discussed above the curriculum content associated with
mathematical enrichment in terms of the two aspects of mathematical
thinking and problem solving. For this content to have meaning, the
learning (and teaching) environment needs to encourage effective
use of the resources so that pupils develop the necessary skills,
strategies and competence to tackle problems and use underpinning
thinking skills effectively. This has implications for the second
thread of mathematical enrichment '?? that of the teaching approach
adopted. There are a number of features of such a teaching
approach, building on the work of Lerman (1999), Romberg (1993) and
Ruthven (1989) and takes a view of pupils constructing their own
learning in a social context, where communication and sharing are
central to mathematical growth and understanding. Aspects of such
an approach include:
- The use of problems which encourage a problem solving approach that in turn supports mathematical thinking and the contextualising of the relevance of mathematical skills and facts (known or to learn).
- Employing the use of low threshold -high ceiling tasks
- Giving pupils time to engage with the problem before moving towards a solution (exploration)
- Focus on "doing mathematics" -pupils taking responsibility for tasks and identifying possible routes to and requirements of solutions rather than being led by the teacher.
- Appropriately targeted mediation that supports entry into problems and development of solutions without leading. Building on pupil discovery and knowledge and making connections (codification)
- Transfer of knowledge which is dependent upon individuals internalising schema with the teacher identifying opportunities.
Mathematical enrichment trails
The trails are a new concept of resource management that are
being developed by the NRICH team, practising teachers and
mathematics educators. They aim to combine related resources
(problems, activities, games, articles, other sites) into a
coherent programme of activities that have problem solving at their
centre and which describe a strand of an enrichment curriculum
aimed at either a particular aspect of mathematical thinking, or a
particular aspect of the curriculum tackled through a problem
solving approach. They also reflect the view of teaching and
learning mathematics outlined above and are being described in
terms of:
- their mathematical content (standard curriculum facts and skills as well as mathematical thinking skills);
- a recommended pathway, or pathways, through the items
- prerequisite knowledge;
- anticipated learning outcomes;
- guidance notes for teachers which reflect the enrichment approach to teaching tha underpins our work
- guidance notes and hints for pupils;
- formative self-assessment mechanisms which will enable medium to long term planning and evaluation.
A trail, for example, might develop and support the work on
number and problem solving through investigating Magic Squares. For
the most able students the work might lead to investigating the
idea of isomorphisms and the underlying structure of some
mathematical problems (looking for pattern and familiarity in
problem solving contexts - "have I seen something like this
before"?). Brighter pupils may also be encouraged to consider
algebraic properties and relationships in this context. A very able
student may begin to generalise and look at "higher order"
mathematics, looking at articles on the subject written by
established mathematicians. Whilst students struggling with
identifying patterns and relationships more generally may benefit
from generalising their findings when working from one magic square
context to another.
A trail on "being systematic" can offer opportunities in a
range of mathematical contexts (number, geometry etc) to take a
systematic approach to solving the problem. Whilst other proof, or
algebra based methods may be just as appropriate in any particular
context, the aim is to use a range of systematic strategies to
access, engage in, and eventually solve, a problem. Work on the
trail may extend over weeks or months or several academic years but
in every case the aim is to give some structure to the development
of the related skills.
The structure of a trail will enable choices concerning the
routes into the resources to reflect the needs of the pupil and
underlying learning theories. Trails aim to "unpick" the
opportunities being offered to pupils to use and develop their
problem solving and other higher order mathematical skills in terms
of content, learning theories and associated teaching styles.
Implications for Implementation
Through the intertwining of the research and development of
the NRICH site, and particularly the trails, the value of this
curriculum innovation is being constantly assessed. All the work is
grounded in appropriate theories as well as research and classroom
experience that not only clarifies and informs the development
itself but throws light on current views and practice with respect
to the role, content and implementation of mathematics enrichment
more generally. As materials are developed and tested this in turn
informs our theoretical framework.
Mediation
An emerging area of interest is the nature and role of
mediation and how mediation can take place, or underpinning
learning theory be reflected, in the materials we produce. Current
small-scale research by members of the NRICH team identifies the
view of problems as rivers to be crossed rather than to be studied
(the process is simply about finding the answer rather that
mathematical discovery). This view acts as a barrier to encouraging
problem solving and mathematical thinking skills. We are currently
undertaking research into the role of mediation and how we can
offer relevant mediation at a distance (Back, J., et al. 2004,
forthcoming).
Conclusion
The clarification of the terms enrichment, mathematical
thinking and problem solving have all led to a clearer
understanding of the potential of NRICH to support mathematical
enrichment more generally, being a vehicle for the many not simply
the few.
Key outcomes:
- establishing a view of enrichment/problem solving /mathematical thinking and reflecting this view within the resources we produce.
- Placing the role of factual knowledge and skills within an enrichment framework both as a precursor and a consequence
- the identification of mediation in a "remote" environment as a key area for our future research
- continuing to reflect the importance of the social role in the construction of knowledge within an online and remote resource
- that issues related to seeing the process and/or solution as the goal rather than the answer is key to our mediation and support work
- that there is a role for assessment and that self and/or peer assessment is an area we need to investigate further.
Impact on the development of the NRICH site
The NRICH had the first phase of its relaunch in January 2004.
The key features of the new site that have been driven by our
research findings are:
- Transparency between levels
- Range of levels and difficulty (challenge level)
- Monthly themes
- Problems also include hints and notes
- Integration of the thesaurus
- Integration of the discussion boards
- Easier access to related material within the archive.
Impact on the development of Trails
- Clear rationale for each trail
- Structure and accompanying documentation that supports learning theories and associated teaching approaches,
- Picking particular mathematical thinking and problem solving schemes as focus for each trail
- Developmental not ad-hoc organisation of resources
- Consideration of the role of mediation and developing mediation strategies.
- The choice of self-assessment as the core assessment strategy.
Bibliography
1. Back, J., Gilderdale, C., Piggott, J., 2004,
forthcoming.
2. Boaler, J., Wiliam, D. et al., 2000, "Students' experiences
of Ability Grouping - disaffection, polarisation and the
construction of failure." British
Educational Research Journal 26( 5): 631 - 648.
3. Brown, M., Millett, A. et al., 2000, "Turning our attention
from the what to the how: the National Numeracy Strategy."
British Educational Research
Journal 26( 4): 457
-471.
4. Cobb, P., Wood, T. and Yackel, E. (1991). "A constructivist
approach to second grade mathematics". In von Glaserfield, E.
(Ed.), Radical Constructivism in
Mathematics Education , pp. 157-176. Dordrecht, The
Netherlands: Kluwer Academic Publishers.
5. Ernest, P., 2000, "Teaching and Learning Mathematics", in
Koshy, V. et al, Mathematics for
Primary Teachers . London Routledge.
6. Koshy, V.,2001, Teaching
mathematics to able children , David Fulton.
7. Lerman, S., 1999, "Culturally Situated Knowledge and the
Problem of Transfer in the Learning of Mathematics", in
Learning Mathematics ,
Burton, L., (Ed), Studies in Mathematics Education Series, Falmer
Press.
8. Lester, F.K.Jr., Masingila, J.O., Mau, S.T., Lambdin, D.V.,
dos Santon, V.M. and Raymond, A.M., 1994. "Learning how to teach
via problem solving". in Aichele, D. and Coxford, A. (Eds.)
Professional Development for
Teachers of Mathematics , pp. 152-166. Reston, Virginia:
NCTM.
9. Mason, J., Burton, L., Stacey, K.,1985, Thinking Mathematically , Prentice
Hall
10. Mayer, R 2002, Mathematical Problem solving, Mathematical
Cognition, 69-72
11. Nardi, E. and Steward, S., 2002, "Part 1: 'I could be the
best mathematician in the world... if I actually enjoyed it'."
Mathematics Teaching
179.
12. Nardi, E. and Steward, S., 2002, "Part 2: 'I'm 14, and I
know that! Why can't some adults work it out?'." Mathematics Teaching 180.
13. Nardi, E. and S. Stewart (2003 forthcoming). "Is
Mathematics T.I.R.E.D.? A profile of quiet disaffection in the
secondary mathmatics classroom." British Educational Research Journal
28( 2).
14. Polya, G., 1957, How to
Solve it , Princeton Paperbacks.
15. Romberg, T., A, 1994, "Classroom instruction that fosters
mathematical thinking and problem solving: Connections between
theory and practice." In A. H. Schoenfeld (Ed.), Mathematical thinking and problem
solving (pp. 287-304). Hillsdale, NJ: Lawrence Erlbaum
Associates.
16. Schoenfeld, A., 1994. "Reflections on doing and teaching
mathematics." In A. Schoenfeld (Ed.). Mathematical Thinking and Problem
Solving . (pp. 53-69). Hillsdale, NJ: Lawrence Erlbaum
Associates.
17. Van Zoest, L., Jones, G. and Thornton, C. (1994). "Beliefs
about mathematics teaching held by pre-service teachers involved in
a first grade mentorship program". Mathematics Education Research Journal
. 6 (1): 37-55.
18. Watson, A., 2001, Changes in mathematical performance of
year 7 pupils who were 'boosted' for KS2 SATs. British Educational
Research Association, Leeds, Education-
