Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Win or Lose?
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
The gambler will have less money than he started with.
Suppose the amount of money before a game is $m$, then:
$m \to 3m/2$ for a win and $m\to m/2$ after losing a game.
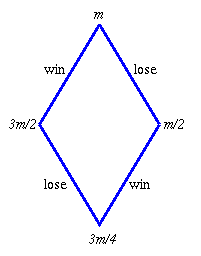
| Values of n | Amount after 2n games: n wins, n losses |
|---|---|
| 1 | $3m/4$ |
| 2 | $m \times 1/2 \times3/2 \times1/2 \times3/2 = (3/4)^2 m$ |
| 3 | $m \times1/2 \times3/2 \times1/2 \times3/2 \times1/2 \times3/2 = (3/4)^3 m$ |
After $n$ wins and $n$ losses he will have $(3/4)^n$ times the money he started with, irrespective of the order in which his wins and losses occur. Eventually he will run out of money as what he has left will be smaller than the smallest coin in circulation.
The diagram was suggested by Roderick and Michael of Simon Langton Boys' Grammar School Canterbury who pointed out that if the gambler went on indefinitely he would, in theory, end up with an infinitely small amount which would be represented by nothing.