 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Numbers as Shapes



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Numbers as Shapes
Here are the numbers $1$ to $6$ drawn using coloured squares:
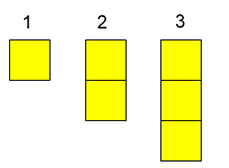
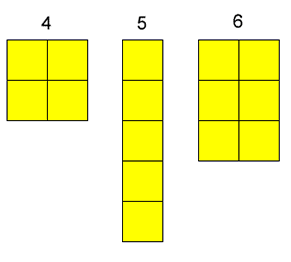
We can call these numbers squares, rectangles or sticks.
$1$ is a square but just a single one.
We can't make $2$ into a square so $2$ is a stick.
We can't make $3 £ into a square or a rectangle so $3% can only be a stick.
We can make $4$ into a square.
We can't make $5$ into a square or a rectangle, so $5$ can only be a stick.
We can't make $6$ into a square, but we can make $6$ into a rectangle.
If you had $7$ yellow squares, what could you make them into? A square, a rectangle or a stick? How about $8$ squares?
Try this with the numbers up to and including $20$.
Which ones can only be sticks?
Which ones can make rectangles?
Which ones are squares?
What do you notice?
This problem was inspired by a session at an ATM conference, led by Tandi Clausen-May.