Hexagon transformations
Can you cut a regular hexagon into two pieces to make a parallelogram? Try cutting it into three pieces to make a rhombus!
Problem
Shown below is a regular hexagon.

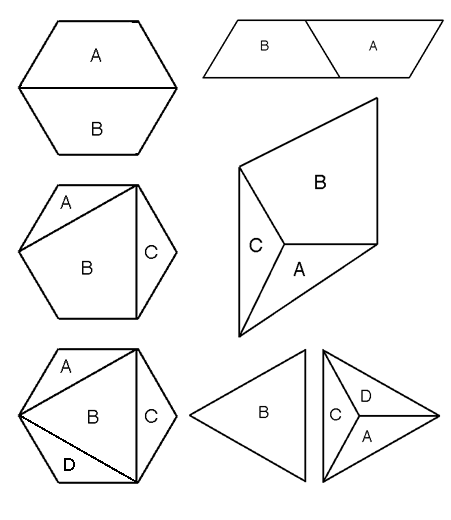
How could it be cut into two pieces which, when put together, make a parallelogram?
How could it be cut into three pieces which, when put together, make a rhombus?
How could it be cut into four pieces which, when put together, make two equilateral triangles?
You could print and cut out hexagons from the sheet of hexagons.
Getting Started
What does a parallelogram/rhombus/equilateral triangle look like?
How could you cut the hexagon into two/three/four pieces?
Student Solutions
Very good solutions to this problem were received from Melanie from West Flegg Middle School, Jack at Smithdon High School and Natalie, Jane and Paul from Methwold High School.
These pictures show how the hexagon can be split:
Teachers' Resources
Why do this problem?
Possible approach
Key questions
