 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Dividing the Field



- Problem
- Student Solutions
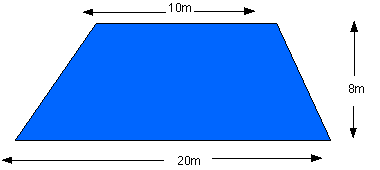
A trapezium has area equal to half the sum of the lengths of the parallel edges times the perpendicular distance between them. The original field has area $h(a+b)/2$ and we are looking for a field with area $h(a+b)/4$.
One solution would be to join the midpoints of the parallel edges with a straight line.There are lots of other solutions. The farmer might want to start from a gate on the edge of length $a$ , at a distance $d$ from one corner, and $(a-d)$ from the other. The dividing line would have to be drawn to a point on the opposite side of the field at a distance $(a+b)/2$ from the corner.
Some people tried to solve a harder problem, that is to split the field by a line parallel to the parallel edges of the field. A particular solution to this was sent in by Jack , Henry, Paul and Matthew from Smithdon High School. It is shown below.
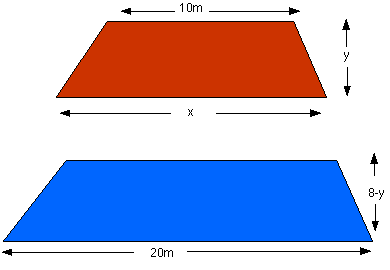
For the first field:
$60=y \times (10-x )/2$- (1)
and for the second field:
$60 = (8-y) \times(20+x)/2$ - (2)
Equation (1) can be rearranged to give:
y = 120 / (10+ x ) - (3)
and equation (2) gives:
120 = (8 - y ) (20 + x ) - (4)
Combining equations (3) and (4) gives:
$120 = (8-120/[10+x])(20+x)$ - (5)
so
$120(10+x)=(8[10+x]-120)(20+x)$
and
$1200+120x=(80+8x-120)(20+x)$
which leads to
$150+15x=(x-5)(x+20)$
and $150+15x=x^2+15x-100)$
so $x^2 = 250$m$^2$
which gives $x=15.8$m (3 s.f.)
and in equation (3) $y=120/(10+x)$ so $y= 4.65$m (3 s.f.)
A further challenge: The solution $x^2 = (a^2 + b^2)/2$ is very special mathematically because it is the same whatever the value of the distance $h$. The language mathematicians use is to say that "the solution is independent of $h$''. Can you explain why this happens in this particular problem? If you want a hint then you could use the fact that when you enlarge a shape with a linear scale factor $s$ then the area is enlarged by a scale factor $s^2$. Look out for more about this problem in a future article on areas and scaling.
Correct solutions to the problem were received from Nicholas - South Greenhoe Middle School ;Heacham Middle School; Lucy and Sarah - Archbishop Sancroft High School