You may also like

problem icon

Pebbles

Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?

problem icon

Great Squares

Investigate how this pattern of squares continues. You could measure lengths, areas and angles.

problem icon

Square Areas

Can you work out the area of the inner square and give an explanation of how you did it?

Areas of Parallelograms

Stage: 3 Challenge Level: Challenge Level:3 Challenge Level:3 Challenge Level:3

Tony sent us his answers to the first parts.

(a) $6$ units squared ($=3\times 2-0\times 5$)
(b) $12$ units squared ($=3\times 4-2\times 0$)
(c) $9$ units squared ($=4\times 3-1\times 3$)
(d)$10$ units squared ($=2\times 3-4\times -1$)

James, Jamie and George from Gillingham School sent us their formula for the area of the general parallelogram.

$$a d-b c$$

Here's one way to work that out.

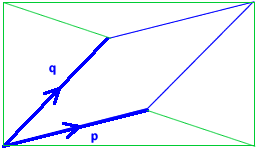
Parallelogram with rectangle and extra lines
Remember that $\mathbf{p}=\left(\begin{array}{c}a \\ b\end{array}\right)$ and $\mathbf{q}=\left(\begin{array}{c}c\\d\end{array}\right)$.
The diagram shows the parallelogram inside a rectangle with base $a+c$ and height $b+d$. This rectangle has area $(a+c)(b+d)$. If we could find the areas of the triangles outside the parallelogram, then we could subtract them from the area of the rectangle to find the area of the parallelogram.
The bottom triangle has height $b$ and base $a+c$, so has area $\frac{1}{2}b(a+c)$.
The triangle on the right has (if you imagine it on its side so that its base is at the bottom) height $c$ and base $b+d$, so has area $\frac{1}{2}c(b+d)$.
The triangle at the top is congruent to the triangle at the bottom (it has been rotated by $180^{\circ}$), so has area $\frac{1}{2}b(a+c)$.
The triangle on the left is congruent to the triangle on the right, so has area $\frac{1}{2}c(b+d)$.
So the area of the parallelogram is $$(a+c)(b+d)-2\times\frac{1}{2}b(a+c) -2\times\frac{1}{2}c(b+d)=a b+b c+a d+c d-a b-b c-b c-c d=a d-b c$$
just as James, Jamie and George said.


The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.