You may also like
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
Six Discs
Six circular discs are packed in different-shaped boxes so that the discs touch their neighbours and the sides of the box. Can you put the boxes in order according to the areas of their bases?
Equilateral Areas
ABC and DEF are equilateral triangles of side 3 and 4 respectively. Construct an equilateral triangle whose area is the sum of the area of ABC and DEF.
Age 14 to 16
Challenge Level
Areas of Parallelograms printable sheet
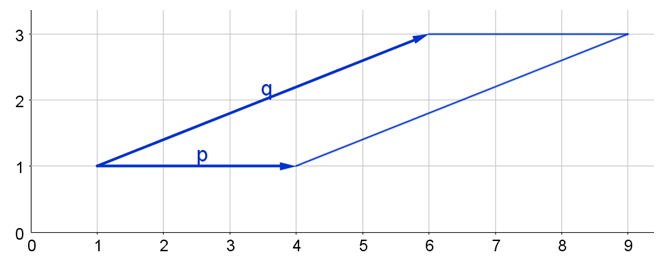
b) $\mathbf{p}=\left(\begin{array}{c}3 \\ 2\end{array}\right), \mathbf{q}=\left(\begin{array}{c}0 \\ 4\end{array}\right)$
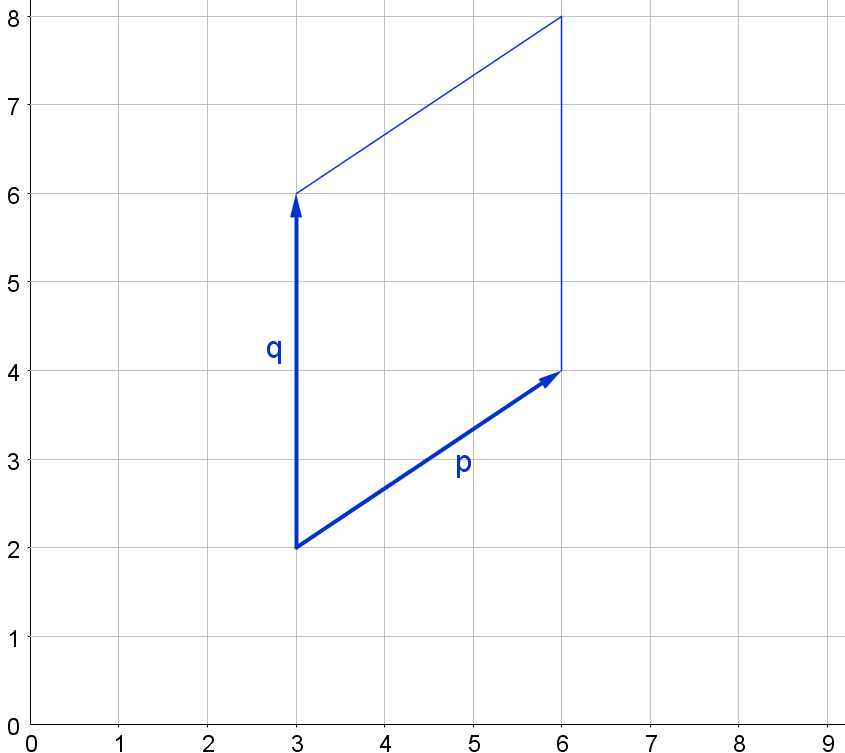
Choose different vectors $\mathbf{p}$ and $\mathbf{q}$, where one vector is parallel to an axis, and find the areas of the corresponding parallelograms.
Can you discover a quick way of doing this?
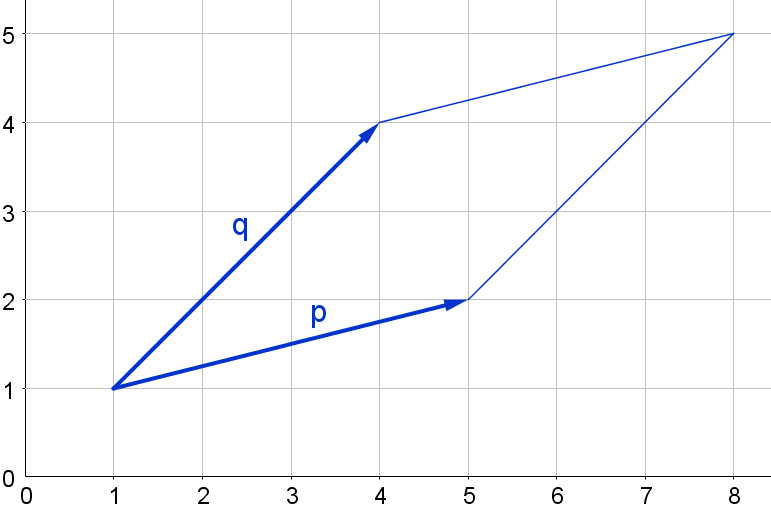
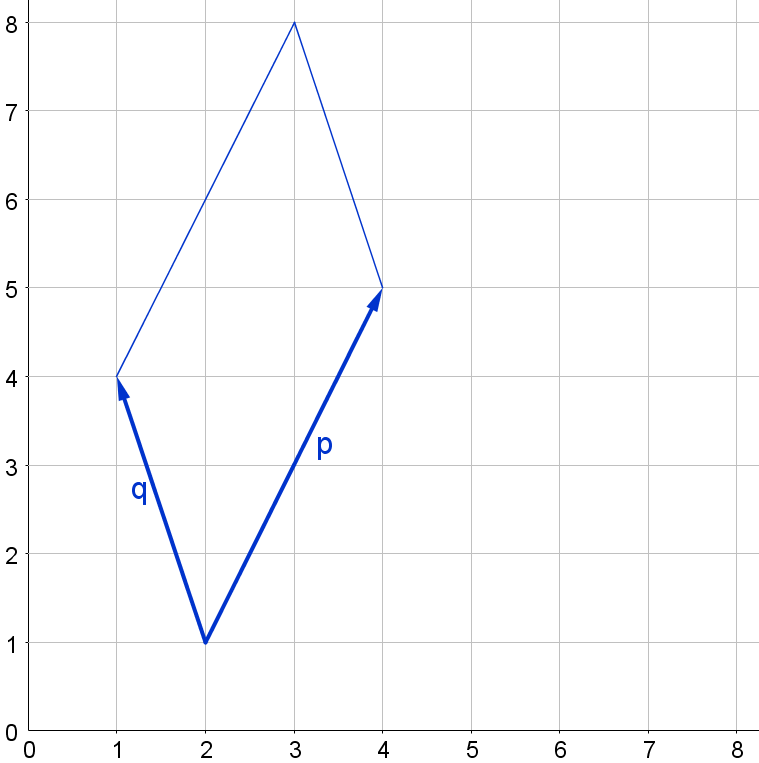
Here are two more parallelograms, again defined by vectors $\mathbf{p}$ and $\mathbf{q}$. This time, neither $\mathbf{p}$ nor $\mathbf{q}$ is parallel to an axis.
Can you find the areas of these parallelograms?
c) $\mathbf{p}=\left(\begin{array}{c}4 \\ 1\end{array}\right), \mathbf{q}=\left(\begin{array}{c}3 \\ 3\end{array}\right)$
d) $\mathbf{p}=\left(\begin{array}{c}2 \\ 4\end{array}\right), \mathbf{q}=\left(\begin{array}{c}-1 \\ 3\end{array}\right)$
Choose some other vectors p and q, where neither p nor q is parallel to an axis.
Can you find a quick way of working out the areas of the corresponding parallelograms?
Can you find the area of the parallelogram defined by the vectors $\mathbf{p}=\left(\begin{array}{c}a \\ b\end{array}\right)$ and $\mathbf{q}=\left(\begin{array}{c}c \\ d\end{array}\right)$?
If you have found a rule, does it ever give you negative areas?
If so, can you predict which vector pairs have this effect?
NRICH is part of the family of activities in the Millennium Mathematics Project.