 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Different by One



If you have not used the Cuisenaire Environment before, you might find it helpful to look at the instructions and video before trying this problem.
Choose two different colours of rod, and make a line of each colour.
Can you make your two lines differ by the length of one white rod?
For example, here are three greens and two yellows. The length of the greens is one less than the length of the yellows.
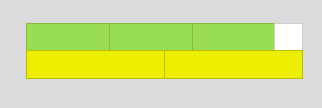
They could also be arranged like this:

Try some different pairs of rods and look for arrangements where the lengths differ by one.
Here are some questions you might like to explore:
If you start with two rods that differ in length by 2, when is it possible to make two lines that differ by 1?
How many of each rod will you need?
What if you could use rods longer than 10, for example 23 and 25? Or 99 and 101? Or...
Once you've found an arrangement where the two lines differ by one, is there a quick way to find other arrangements with the same colour rods that also differ by one?
What if you start with two rods that differ in length by 3? By 4?