 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Different by One



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This was a challening problem! Well done to everyone who shared their thoughts and solutions with our team.
Students at Long Field Academy began by exploring this problem using the Cuisenaire environment. Theo explained how to find rods that differ in length by one:
To create a difference of one white rod it is all about times tables. If you were to have three rods of three, which would be 3x3=9, and then if you had two rods of four which is 2x4=8 which creates one rod difference. Another way you could do it is 7x3 and 4x5 which would be 21 and 20.
.png)
Caleb from Kilvington Grammar in Australia used rods that differ in length by 2, and explained when it is impossible to get a difference of 1:
To solve this problem, we start with two terms: $x$ and $(x-2).$ The first thing I figured out is that $x$ cannot be even, because then both terms would be even, and anything multiplied by an even number is an even number, therefore not giving us a difference of $1,$ which would only appear in an even and an odd number. Also, using the equation below, you wouldn't multiply the number by a whole number. I don't like my solution, because I just used trial and error, but here it is:
$x\times\frac{x-1}2 - (x-2)\times\frac{x+1}2=1$ [that is, $\frac{x-1}2$ rods of length $x$ and $\frac{x+1}2$ rods of length $(x-2)$ have a difference of $1$]
Yinuo from HD Ningbo School in China had the same formula, but Yinuo called the lengths $l_1$ and $l_2$ instead of $x$ and $(x-2)$. Yinuo proved that the formula really does give a difference of $1$:
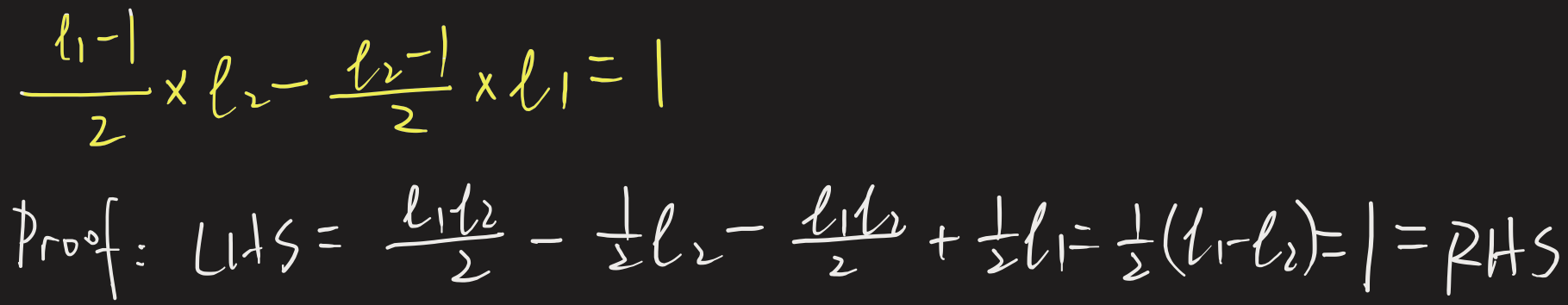 (remember that $l_1 - l_2 = 2$)
(remember that $l_1 - l_2 = 2$)
Mahdi from Mahatma Gandhi International School proved that you can never make a difference of $1$ when the rods differ by $2$ and both have even length:
(Mahdi is talking about the difference multiplied by 2)
Mahdi then considered the case where the rods have odd lengths, and found an alternative proof to the ones shown above. Click to see Mahdi's work.
note: the denominator should say "Number of numbers", or something similar, not "Difference"
Yinuo then thought about rods with lengths that differ by 3 and 4. This is Yinuo's work:

i) Two rods that are multiples of $3$
No arrangement
ii) $l_1-l_2=3,$ $l_1$ and $l_2$ are both greater than multiples of $3$ by $1,$ e.g. $1, 4$ and $4,7$
In the equation below, Yinuo writes $3n+1$ in brackets to add information about $l_1$ and $l_2$. It does not mean that $l_1$ and $l_2$ are multiplied by $3n+1$.
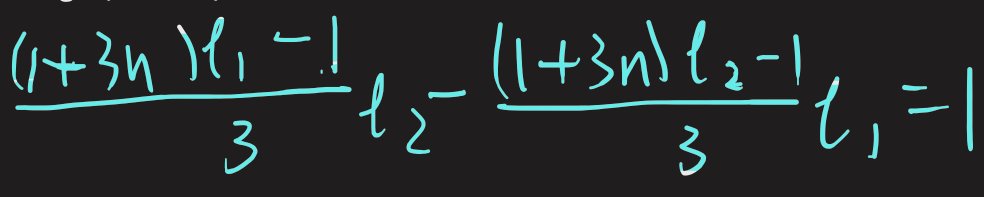
Click to see a proof.
$\begin{split}\frac{l_1-1}3l_2 - \frac{l_2-1}{3}l_1 &= \tfrac{1}{3}\times\left((l_1-1)l_2 - (l_2-1)l_1)\right)\\
& =\tfrac{1}{3}\left(l_1l_2-l_2 - l_1l_2+l_1\right)\\
&=\tfrac{1}{3}\left(l_1-l_2\right)\\
&=1\end{split}$
iii) $l_1$ and $l_2$ are both less than multiples of $3$ by $1,$ e.g. $2, 5$ and $5,8$ (equivalently these are $2$ more than a different multiple of $3$)
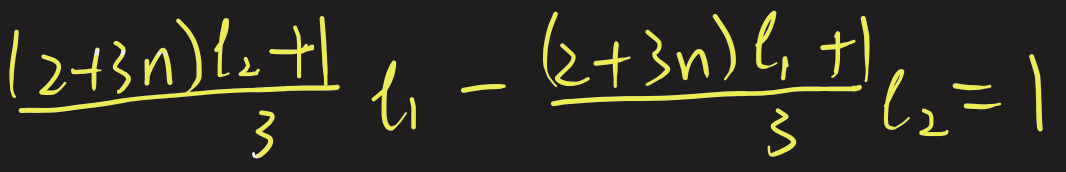
Click to see a proof.
$\begin{split}\frac{l_2+1}{3}l_1 - \frac{l_1+1}3l_2 &= \tfrac{1}{3}\times\left((l_2+1)l_1 - (l_1+1)l_2)\right)\\
& =\tfrac{1}{3}\left(l_1l_2+l_1 - l_1l_2-l_2\right)\\
&=\tfrac{1}{3}\left(l_1-l_2\right)\\
&=1\end{split}$

i) Two rods have even lengths
No arrangements
ii) $l_1-l_2=3,$ $l_1$ and $l_2$ are both greater than multiples of $4$ by $1,$ e.g. $1, 5$
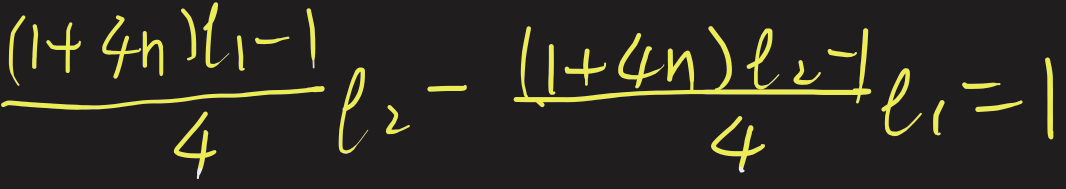
iii) $l_1-l_2=3,$ $l_1$ and $l_2$ are both smaller than multiples of $4$ by $1,$ e.g. $3, 7$
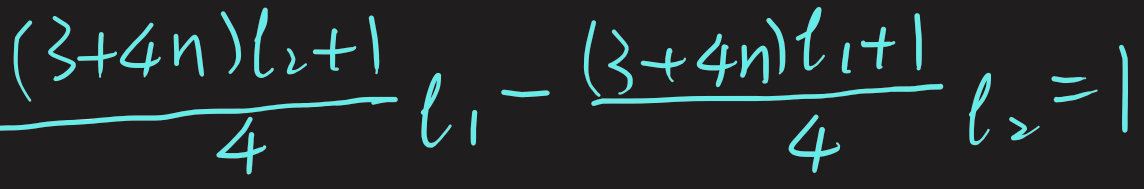

Yinuo says that possible arrangements exist "periodically". Mahdi showed how to use one arrangement which gives a difference of $1$ to find other arrangements which also give a difference of $1$:
Let the two rods be of difference $d.$ Thus let the lengths be $k, k+d.$
Let there be $x$ number of $k$ rods and $y$ number of $d$ rods which give a difference of $1.$
To get infinite pairs:
Find the lowest common multiple (LCM) of $k$ and $k+d$. If they are mutually prime, the LCM is $k(k+d)$ (if they have no common factors, they are said to be coprime, which is sufficient here)
Adjust $n$ to any value and get infinite pairs.
$\left(x + n\times\frac{\text{LCM}}k, y + n\times\frac{text{LCM}}k\right)$
If they are prime (or coprime):
$\left(x + n(k + d), y + nk\right)$