You may also like
Doodles
Draw a 'doodle' - a closed intersecting curve drawn without taking pencil from paper. What can you prove about the intersections?
Russian Cubes
I want some cubes painted with three blue faces and three red faces. How many different cubes can be painted like that?
Picture Story
Can you see how this picture illustrates the formula for the sum of the first six cube numbers?
Age 14 to 16
Challenge Level
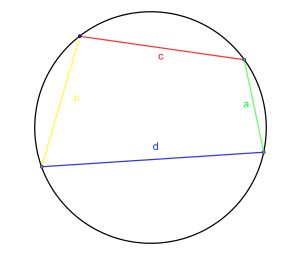
Draw a circle with radius $1$ unit. Choose any four points on
the circumference and join them together to form a
quadrilateral.
Label the sides: $a$ is the shortest, $b$ is the next shortest, then $c$, and finally $d$ is the longest side (it is possible to have two sides of equal length).
What is the maximum length that the shortest side $a$ could be?
Side $b$ must be less than a certain value - what value?
What is the maximum length that the longest side $d$ could be? Is it possible for $c$ and $d$ both to be this maximum length?
Copyright © 1997 - 2023. University of Cambridge.
All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.
NRICH is part of the family of activities in the Millennium Mathematics Project.