 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Long Short



- Problem
- Student Solutions
- Teachers' Resources
This solution is from Tony Cardell, age 15, State College Area High School, PA, USA.
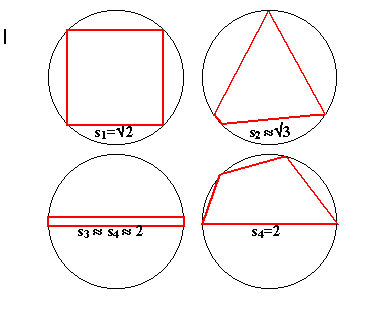
We investigate quadrilaterals inscribed in the unit circle. The sides of the quadrilateral $s_1$, $s_2$, $s_3$, $s_4$, subtend angles $\theta_1, \theta_2, \theta_3, \theta_4$ at the centre of the circle where $\theta_1 \leq \theta_2 \leq \theta_3 \leq \theta_4$. Now $\theta_1 \leq 90^\circ$ so the the largest value of
$s_1$ is when the quadrilateral is a square.First investigating an inscribed quadrilateral where all sides are equal, $s = s_1 = s_1 = s_3 = s_4$ , which is a square with diagonal of length 2 units, we find that the side length of this square is given by $2s^2 = 4$, so that
\( s = \sqrt{2}\).
If we made $s_1$ any larger, clearly the larger square that is formed will not fit in the circle.Now imagine an equilateral triangle inscribed in the unit circle. The angle at the centre is \(120^\circ \)
and the side length is \( s = \sqrt{3}\) . We can make a quadrilateral by slightly distorting this triangle and introducing another very short side. Therefore, in our quadrilateral, the second side must always be less than \( s = \sqrt{3}\) since if not side one would have length zero and you would not have a quadrilateral. However side one can get very small, approaching zero, so that side 2 can approach \( s = \sqrt{3}\) . We can have one very short side (almost zero) one just less that \( s = \sqrt{3}\) and the other two equal to \( s = \sqrt{3}\) .Side 3 can approach length 2 because we can make a quadrilateral with sides three and four very close to 2 and sides one and two very close to zero. As sides one and two approach zero, sides three and four clearly approach 2, the diameter of the unit circle.
Finally, at its maximum, side 4 can be 2 when side 4 is the diameter of the unit circle. The other sides will fit into one of the halves of the circle because you can make them as small as you want. Any line longer than 2 units will extend outside the circle so side four cannot be longer than 2 units.