Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Screen Shot
Age 14 to 16
Challenge Level 





A moveable screen slides along a mirrored corridor towards a
centrally placed light source. A ray of light from that source is
directed towards a wall of the corridor, which it strikes at
$45^\circ $ before being reflected across to the opposite wall and
so on until it hits the screen.
If the screen is $20$ metres down the corridor from the light source and if the corridor is $2$ metres wide, find the position on the screen where the point of light appears.
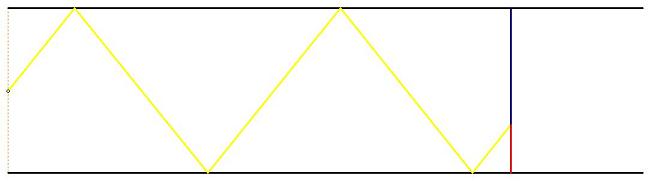
Part Two: Now remember that the screen is moveable. The distance, $d$, of the screen down the corridor can change, so the position where the point of light appears on the screen will depend on $d$. Can you find a function, expressing the position of the light on the screen in terms of $d$?
Part Three: If the ray leaves the source making an angle $\theta$ with the direction of the corridor, and the distance, $d$, of the screen down the corridor can still change, the position where the point of light appears on the screen will depend on $d$ and on $\theta$ . Can you find this function?
If the screen is $20$ metres down the corridor from the light source and if the corridor is $2$ metres wide, find the position on the screen where the point of light appears.
Part Two: Now remember that the screen is moveable. The distance, $d$, of the screen down the corridor can change, so the position where the point of light appears on the screen will depend on $d$. Can you find a function, expressing the position of the light on the screen in terms of $d$?
Part Three: If the ray leaves the source making an angle $\theta$ with the direction of the corridor, and the distance, $d$, of the screen down the corridor can still change, the position where the point of light appears on the screen will depend on $d$ and on $\theta$ . Can you find this function?