You may also like

problem icon

Fixing It

A and B are two fixed points on a circle and RS is a variable diamater. What is the locus of the intersection P of AR and BS?

problem icon

OK! Now Prove It

Make a conjecture about the sum of the squares of the odd positive integers. Can you prove it?

problem icon

Summats Clear

Find the sum, f(n), of the first n terms of the sequence: 0, 1, 1, 2, 2, 3, 3........p, p, p +1, p + 1,..... Prove that f(a + b) - f(a - b) = ab.

Cyclic Triangles

Age 16 to 18 Challenge Level:

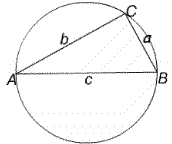
Triangle ABC inscribed in circle with diameter AB
A triangle $ABC$ is inscribed in a circle with $AB$ as diameter. Find the maximum value of $AC + CB$.

Now generalise your result to the case where $AB$ is fixed but not a diameter of the circle.

Make and prove a conjecture about the cyclic quadrilateral inscribed in a circle of radius $r$ that has the maximum perimeter and the maximum area.




Here is an alternative Flash interactive.
If you can see this message Flash may not be working in your browser
Please see http://nrich.maths.org/techhelp/#flash to enable it.
The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.
Copyright © 1997 - 2018. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.