Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cyclic Triangles
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Congratulations to Curt, Reigate College and to Andrei, Tudor Vianu National College, Bucharest, Romania for you solutions to this problem
When AB is a diameter angle $ACB$ is 90 degrees so we can use Pythagoras' Theorem. The area of the triangle is given by $\textstyle{1\over 2}ab = \textstyle {1\over 2}ch$ where $h$ is the length of the perpendicular from $C$ to $AB$. Then
$$(a+b)^2=a^2+b^2+2ab=c^2+2ch.$$
Thus $(a+b)^2$ is a maximum when $h$ is a maximum and equal to the radius of the circle $\textstyle {1\over 2}c$ . So the maximum value of $a+b$ is $c\sqrt 2$.
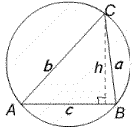
When $AB$ is not a diameter we have (using the Cosine
Rule):
$$\eqalign{ (a+b)^2 &= a^2 +b^2 + 2ab \cr &= c^2 +
2ab\cos \angle ACB +2ab \cr &= c^2 +2ab(1+\cos \angle ACB) \cr
&=c^2 +4ab \cos^2 \textstyle {1\over 2}\angle ACB.}.$$
As the area of triangle $ACB$ is given by $\Delta = \textstyle
{1\over 2} ab\sin \angle ACB$ we have
$$\eqalign { (a+b)^2 &= c^2 + {8\Delta \cos^2
\textstyle{1\over 2}\angle ACB \over \sin\angle ACB} \cr &= c^2
+ 4\Delta \cot \textstyle {1\over 2}\angle ACB }.$$
If we keep $A$ and $B$ fixed and vary $C$ then, as $c$ and
$\angle ACB$ are constant, and the area of the triangle $\Delta$ is
a maximum when $h$ is a maximum, it follows that $a + b$ is a
maximum when $h$ is a maximum, that is when $a=b$ and the altitude
of the triangle drawn from $C$ to $AB$ is a line of symmetry of the
triangle. In this case
$$a=b={c\over 2\sin \textstyle {1\over 2}\angle ACB}.$$
Conjecture: Let $Q$ be a variable cyclic quadrilateral in a
circle of radius $r$. Then the area and the perimeter of $Q$ will
be a maximum when $Q$ is a square; that is when each of the
diagonals of the quadrilateral is a diameter and each diagonal
bisects of the other diagonal at right angles.