Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Just Rolling Round
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
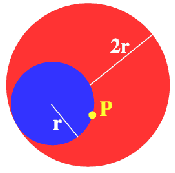 |
Why do this problem?
In this
problem , the interactivity enables learners to experiment and
make their own conjectures about the locus. The proof requires only
simple geometrical reasoning involving circle theorems and arc
lengths.
Possible approach
Learners might first experiment with the interactivity and
make a conjecture about the locus, then try to prove their
conjecture.
|
Key question
We know the small circle rolls around inside the big one. What can we say about arc lengths?
Possible support
Learners might draw their own interactive diagrams using Geogebra.
Ask about how far a bicycle goes forward when the wheels rotate through exactly one revolution.
What about a revolution by a given angle?
What if the road was curved?
Possible extension
See the problem Illusion.

