You may also like
Roaming Rhombus
We have four rods of equal lengths hinged at their endpoints to form a rhombus ABCD. Keeping AB fixed we allow CD to take all possible positions in the plane. What is the locus (or path) of the point D?
Triangles and Petals
An equilateral triangle rotates around regular polygons and produces an outline like a flower. What are the perimeters of the different flowers?
Age 14 to 16
Challenge Level
|
Tomas of Malmsbury School, Mark of The
British School of Manilla and Herbert of Sha Tin College, Hong Kong
sent good solutions to this problem. Well done all of
you.
$P$ is a point on the circumference of a circle radius $r$
which touches another circle radius $2r$ on the inside. The smaller
circle rolls, without slipping, around the inner circumference of
the larger circle.
The point $P$ is a fixed point on the smaller circle which
moves as the small circle moves. The point $P_o$ is the position of
$P$ when $P$ is at the point of contact between the two circles.
Consider the general position where the point of contact is the
point $C$ but here we do not assume that $P_1$ is the position of
the point $P$.
 |
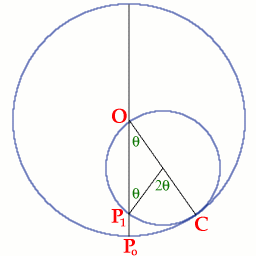By showing that the lengths of the arcs $P_oC$ and $P_1C$ are
equal, we shall prove that $P_1$ must be the position of the point
$P$ when the point of contact is at $C$. Hence we shall show that
$P$ must always lie on the diameter of the large circle through
$OP_o$.
Let $M$ be the centre of the small circle, then $MO = MP_1 =
MC = r$ and the triangle $OMP_1$ is isosceles. Hence $$\angle MOP_1
= \angle MP_1O = \theta$$ $$\angle P_1MC = \pi - (\pi - 2\theta) =
2\theta.$$ Hence, using the formula "arc length = radius x angle at
the centre of the circle": $$P_0C = (2r)(\theta) = 2r\theta$$ and
$$P_1C = (r)(2\theta) = 2r\theta.$$ Hence $P$ must be at the point
$P_1$ because the circle rolls without slipping, which shows that
the locus of P is the diameter of the larger circle.
Copyright © 1997 - 2021. University of Cambridge.
All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.
NRICH is part of the family of activities in the Millennium Mathematics Project.