Baby Circle

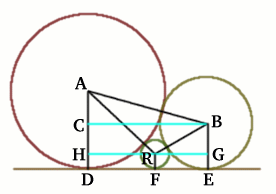
Rosalind of Madras College sent in this solution, well done Rosalind.

All three circles touch each other and have a common tangent $DFE$. The radius of the baby circle is $r$ and the radii of the other circles are $BE = 1$ unit and $AD = 2$ units. So $AC = 1$ unit, $AB = 3$ units, $AH = 2 - r$, $AR = 2 +r$, $BR = 1 + r$ and $BG = 1 - r$. Using Pythagoras Theorem: $$\eqalign{ \; RG &=& \sqrt{(1+r)^2 - (1-r)^2} = \sqrt{4r} = 2\sqrt{r} \\ \; HR &=& \sqrt{(2+r)^2 - (2-r)^2} = \sqrt{8r} = 2\sqrt{2r} \\ \; CB &=& 2\sqrt{2} = DE \\ RG + HR = CB &\Rightarrow& 2\sqrt{r} + 2\sqrt{2r} = 2\sqrt{2}.}$$ This gives $\sqrt{r}(1+\sqrt{2}) = \sqrt{2}$ and hence by squaring $$\eqalign{ r &=& \frac{2}{3+2\sqrt{2}} \\ \; &=& \frac{2(3 - 2\sqrt{2})}{(3+2\sqrt{2})(3-2\sqrt{2})} \\ \; &=& \frac{6 - 4\sqrt{2}}{9 - 4\times2} \\ \; &=& 6 - 4\sqrt{2}}$$ So the radius of the `baby circle` is $6 - 4\sqrt{2}$.