Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tubular Stand
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
There were a number of partial solutions but this well explained one is almost entirely the work ofAndrei of Tudor Vianu National College and shows how "obvious" the answer is with a little visualising and careful reasoning.
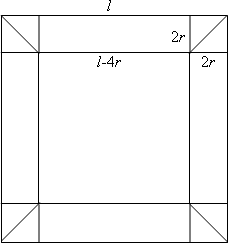
Let $l$ be the exterior length of the cylinders and $r$ - the radius of the cylinders.
In the first solution, I have $4$ cylinders (the $4$ squares length $l-4r$ and $2r$) and $8$ half-cylinders - cylinders cut through the diagonal (the 8 small right-angled triangles from the figure).
Each of the four cylinders has the volume: $ V_1 = \pi r^2 (l - 4r)$
Each of the half-cylinders has a volume of half a cylinder: $ V_2 = \frac{1}{2} \times \pi r^2 \times 2r = \pi r^3$ Now, the total volume of the tubular stand is: $ V = 4 \times V_1 + 8 \times V_2 = 4\pi r^2 (l - 2r) $
With the second method, I arrange the $8$ half-cylinders to make $4$ bigger cylinders, and these $4$ to the bigger ones. The height of one 'big' cylinder is $(l - 2r)$, and the total volume is: $$ V = 4 \pi r^2 (l - 2r) $$ which is exactly the result obtained above. Substituting the numerical values: $l = 10 \; \text{cm}$ and $r =0.5 \; \text{cm}$, I obtain:
$$ V = 4 \pi \times 0.25 \times(10 - 1) = 9 \pi = 28.27 \; {\text{cm}}^3 $$
If the volume wood would be double $(18 \pi)$, then the outside dimension of the dowel would be: \begin{eqnarray} 18 \pi &=& 4\pi \times 0.25 (l -1) \\ l - 1 & =& 18 \; \text{cm}\\ l &=& 19 \; \text{cm}\end{eqnarray} If the volume of wood would be the same but the radius would be $1 \; \text{cm}$, then the outside dimension would be: \begin{eqnarray} 9 \pi &=& 4\pi (l - 2) \\ l - 2 &=& \frac {9}{4} \\ l &=& 4.25 \; \text{cm}\end{eqnarray} The general formula for the volume of the dowel (proved above) is: $$ V = 4 \pi r^2 (l - 2r) $$ One could see that the volume is proportional to the square of the radius, and in the limit of long outside dimensions, proportional to the outside dimension.