Tubular Stand

A square stand designed to protect surfaces from hot pans is made from four $10 \; \text{cm}$ long pieces of cylindrical wooden dowel joined at the corners with $45$ degree mitres.

If the radius of the dowel used to make a stand is $0.5 \; \text{cm}$, what is the volume of wood used?




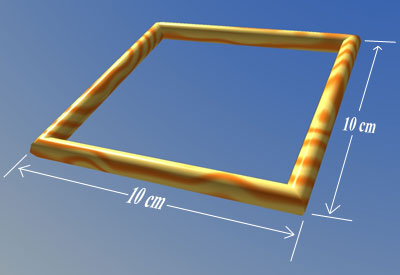
If I doubled the volume of wood used but did not change the radius of the dowel - what would the outside dimension of the stand be?

If, instead, I doubled the radius of the dowel but kept the same volume of wood, what would the outside dimension of the stand be then?

By looking in more detail at the effects of changing one of the variables at a time, can you describe any relationships between the volume of wood, the radius and the length of the dowel used?