Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Squirty
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thanks to Andrei of School 205 Bucharest for this well explained solution.
- First, I drew a line $HG$, perpendicular on $P$, and a line through H, parallel with $PR$.
- On it, I took a segment $HE$ of the same length with $HO$.
- Then I finished drawing the square $HEFO$, drawing $EF$ perpendicular on $PR$. The line PE intersects $QR$ in $A$.
- From $A$ I drew a parallel to $PR$ (let the intersection point with $PQ$ be $D$), and a perpendicular to $PR$ (let the intersection point with $PR$ be $B$).
- This way I found 3 vertices of the rectangle $ABCD$, and I finished the rectangle finding the vertex $C$ on $PR$, so that $CD$ is perpendicular to $PR$.
The rectangle $ABCD$ is a square because:- Triangles $PEF$ and $PAB$ are similar, they are both right-angled triangles, with a common angle. The similarity ratio is: $${{PE}\over{PA}} = {{EF} \over {AB}}$$ Triangles $PEH$ and $PAD$ are similar, because angles $PEH$ and $PAD$ are equal and $HPE$ is a common angle. The similarity ratio $$\frac{PE}{PA} = \frac{HE}{AD}$$ From $(1)$ and $(2)$ $$ \frac{AB}{EF} = \frac{AD}{HE}$$ As $HE=EF$ (sides of a square) Therefore $ AB =AD$ $ ABCD$ is a rectangle with two adjacent sides equal
Therefore $ ABCD$ is a square.
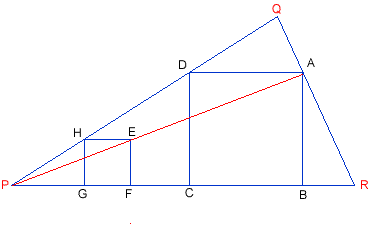
Now, the construction of the inscribed square must be done in the following steps:
- Choose a point $H$ on side $PQ$, near $P$
- Draw line $HG$, perpendicular on $PR$
- Take the distance $HG$ as the compass distance, and draw a circle arc, with centre $G$. $F$ is the point of intersection of this arc with $PR$.
- Construct two circle arcs with centres $F$ and $H$ (with the same radius as before). Their intersection is point $E$, and $EFGH$ is a square.
- Draw line $PE$. Let the intersection point of this line with side $QR$ be $A$.
- Draw from $A$ parallel to $EF$ and $HE$. Their intersections with $PR$ and $QP$ are points $B$ and $D$ respectively.
- Draw from $D$ a parallel to $AB$. Its intersection with $PR$ is $C$.
- $ABCD$ is the square to be found.
Note
The choice of point $P$, so that $E$ is interior to the
triangle $PQR$ is not a restrictive condition, the construction is
the same if $E$ is exterior to triangle $PQR$.