Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Squirty
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Can you draw a square ABCD with BC on the base PR of the triangle and the vertex D on the side PQ using ruler and compasses?
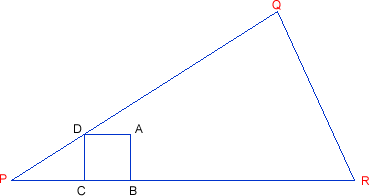
What happens to the point A as you enlarge the square? The interactivity may help. Move Q to specify your triangle, and then move D to enlarge the square.
How can you use this to help you draw the square you require?