 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
A Square in a Circle



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We had a large number of interesting ideas sent in for this activity, too many to show here, but it revealed that many pupils are still working to understand the names and properties of shapes as well as the methods for calculating area.
Isaac from Ecole Internationale de Ferney-Voltaire sent in this thorough explanation of what is involved.
The answer to the first part of the problem is that the shape that he has made is a square. This is so because there is an equal distance from the points $12$ to $3$, $3$ to $6$, $6$ to $9$, and $9$ to $12$. A polygon of four equal sides creating four right angles is by definition a square.
In this problem we are given the diameter of the circle that the square was made from, and asked to give the area. In this problem the diameter is given by connecting the points of $12$ and $6$. Doing this also divides the square in half giving two right isosceles triangles. We also know that the diameter is $10$ cm. Using the Pythagorean theorem we can find the two legs of a triangle that is half the square. The Pythagorean theorem states that $A^2 + B^2 = C^2$. In this case we can adjust it to $A^2 + A^2 = C^2$, since all sides are equal. We know that the hypotenuse is $10$ cm long so $A^2 + A^2 = 10^2 (or 100)$. If we divide $100$ by $2$ we then get $50$, so $A^2 (or 50) + A^2 (or 50) = C^2 (or 100)$. To find what A is we must find $\sqrt50 (or A^2)$. $\sqrt50$ is $7.071067812$ then just find $7.071067812$ x $7.071067812$ which is really unnecessary since we had to find the square root of $50$ to get $7.071067812$.
In conclusion the area of the square located inside the clock is $50$ cm squared.
The answer to the third question is really quite simple. We know that we can only line up seven $1$cm by $1$cm tiles on one side of the square since the sides length is $7.071067812$ and we are not allowed to go outside the line. This is the same for all the sides since the shape is a square. So $7$ tiles x $7$ tiles is $49$ tiles.
From Anna, Elsa, Huw and Molly from the Extension Maths Group, St Nicolas C of E Junior School, Newbury we had the following good account sent in as a document.
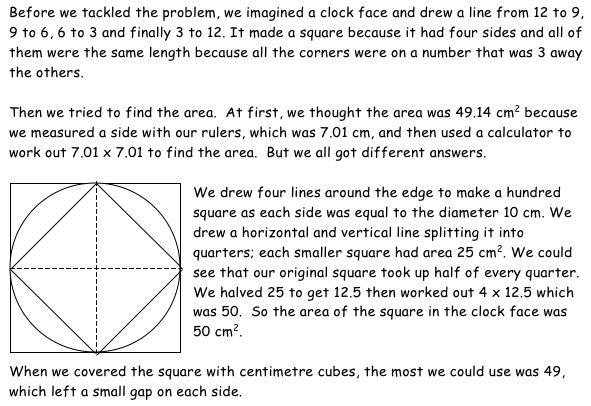
From Sarah at the Pioneer Valley Performing Arts Charter Public School, Massachusetts U.S.A. we had another well thought out account of the problem.
The problem is that Harry drew a picture of a clock. The clock had a diameter of $10$ cm. He drew a straight line from the $12$ to the $3$, from the $3$ to the $6$, from the $6$ to the $9$, and then from the $9$ back to the $12$. I needed to figure out what shape was drawn, and the number of whole centimeter tiles that could fit into Harry's shape.