Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
A Square in a Circle
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
A square in a Circle
Harry had a circle which was marked with twelve numbered dots to help him draw clock faces. The circle had a diameter of $10$ cm.
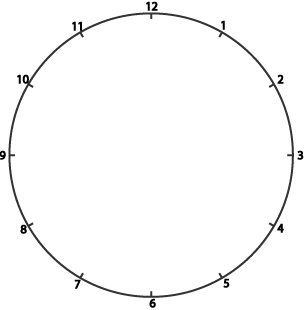
Harry drew lines from the $12$ to the $3$, from the $3$ to the $6$, from the $6$ to the $9$, and then back from the $9$ to the $12$.
What shape had he drawn?
Find the area of the shape.
Harry had lots of centimetre square tiles.
He covered as much of his shape as he could with whole tiles without going over the edge.
What was the largest number of whole tiles he could fit in?
Why do this problem?
This problem requires visualisation as well as calculation, and is an interesting way of doing some work on squares and area. Learners will need to know how to find the area of a rectangle. It is also a useful reminder for those children who insist that a square which has been rotated by
$45^\circ$ is a 'diamond' or rhombus!
(This problem does not require knowledge of Pythagoras' theorem.)
Possible approach
You could start with the whole group by asking them to visualise a clock face. Ask them to imagine joining the $12$ to the $3$, the $3$ to the $9$ and then the $9$ to the $12$. What shape have they made? Then try the $1$ to the $4$, the $4$ to the $7$, the $7$ to the $10$ and the $10$ to the $1$. Finally try the $11$ to the $5$, the $5$ to the $7$ and then the $7$ to the $11$.
After this tricky exercise in visualisation, put a clock face on the board and draw out the shapes. The two triangles are different and learners can be asked about them.
You could then introduce the actual problem which may be best done in pairs so that children are able to talk through their ideas with a partner. Have some copies of this sheet (two copies of the clock face), squared paper and scissors available. Some
learners might find it useful to draw out a circle with a radius of $5$ cm on squared paper (centred on the corners of four of the squares), then count squares.
The second part of the question is slightly more difficult. A reminder of the square numbers might be helpful.
At the end of the lesson a discussion of how the group found the solutions could prove very useful to both each other and you (for assessing their understanding).
Key questions
What shape have you drawn?
Have you drawn in any other lines?
What length are the diagonals of the square?
What length are the sides of that triangle?
What is the nearest square number to that?
Have you thought of starting to tile in one of the corners?