Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Biggest Enclosure
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
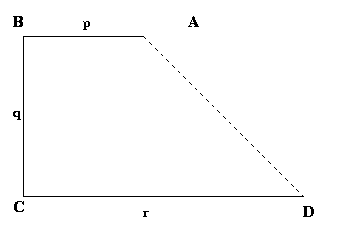 |
Shaun of Nottingham High School and also Ben and Thomas sent in good solutions to this problem. Here is Shaun's solution.
There are three possibilities we must consider, in each one the 'middle' fence (vertical in the diagram ) is one of $p$, $q$ or $r$. Interchanging the horizontal fences either side makes no difference to the area of the shape, it is just being flipped vertically. Remember the area of a trapezium can be expressed as ${1\over 2}(a+b)h$, where $a$ and $b$ are parallel sides, and $h$ the distance between them. |
This means we can express the areas of the three possible shapes as:
$$\frac {1}{2}(p+q)r, \frac {1}{2}(q+r)p, \frac {1}{2}(r+p)q.$$
Let's compare the first two. As $qr> qp$ we have $qr + pr > qp + pr$ and so
$${1\over 2}(p+q)r > {1\over 2}(q+r)p.$$
I hope you can see an identical argument can be used to compare the other pairings of expressions for area, and we end up with:
$${1\over 2}(q+p)r > {1\over 2}(p+r)q > {1\over 2}(r+q)p.$$
So the fences should be arranged with $r$ being the middle one in order to enclose the maximum area.