Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Biggest Enclosure
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
Three fences of lengths $p$, $q$ and $r$ with $p< q< r$ are arranged to form three sides $AB$, $BC$ and $CD$ of a field $ABCD$ with right angles at $B$ and $C$.
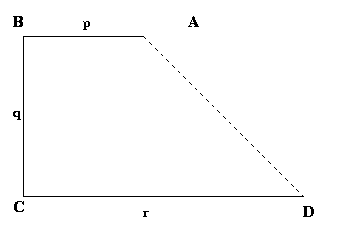
The diagram shows one possibility but the fences can be exchanged to make different enclosures.
The enclosure is completed by joining $A$ and $D$.
How should the rods be arranged to make the area of the enclosure as big as possible?