You may also like
Degree Ceremony
What does Pythagoras' Theorem tell you about these angles: 90°, (45+x)° and (45-x)° in a triangle?
Ball Bearings
If a is the radius of the axle, b the radius of each ball-bearing, and c the radius of the hub, why does the number of ball bearings n determine the ratio c/a? Find a formula for c/a in terms of n.
Age 16 to 18 Challenge Level:
$ABCD$ is a rectangle where $BC$ = $3AB$. $P$ and $Q$ are points on $BC$ such that $BP$ = $PQ$ = $QC$.
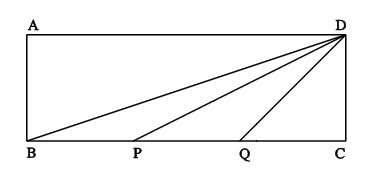
Show that: angle $DBC$ + angle $DPC$ = angle $DQC$
Generalise this result.
N.B. This problem can be tackled in at least 8 different ways using different mathematics learnt in the last two years in school and earlier. The methods are essentially the same when viewed from a more advanced perspective.
Copyright © 1997 - 2018.
University of Cambridge. All rights
reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.
NRICH is part of the family of activities in the Millennium Mathematics Project.