 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
4 Dom



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
4 Dom
Use these four dominoes to make a square that has the same number of dots on each side.
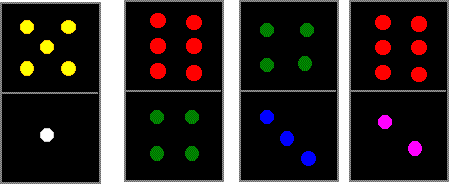

We would love to see pictures of your completed square but please also tell us what you do to try and solve the challenge.
Here is an interactive you might like to use to try out your ideas.
Click on a domino to rotate it. Use the white x to move a domino around.
Why do this problem?
This problem provides a great opportunity to focus on key problem-solving skills (e.g. trial and improvement) as the level of challenge is provided by there not being an obvious way to solve it, rather than from the number or calculation content. Having said that, however, it does give learners a good reason to develop and use appropriate vocabulary associated with number/calculation. Dominoes are such a versatile resource and having the real thing would be very useful. In this case, the interactivity almost demands more careful planning of where to place a domino compared with use of physical dominoes themselves, and this gives the learner thinking time and space for noticing. 'Noticings' spark children's curiosity, which gives them the motivation to persevere with the task.
Possible approach
One way to engage learners in the task would be to use the interactivity to display four dominoes in a square, but without having equal numbers of dots on all four sides. Invite children to consider what they see and give them time to discuss in pairs before taking contributions within the whole group. Welcome all noticings and once the class has shared their observations, use children's comments to introduce the task itself. You may want to establish the number of dots on each side of your square so that learners have a good understanding of the task.
Ideally, pairs of children will have access to the interactivity on a laptop, computer or tablet, and dominoes, so that they can decide which manipulative they would prefer (or use both). You could print off copies of the printable sheet from the top of the main Problem page to give to pairs. Give them time to begin the task and then draw everyone together for a mini plenary to talk
about how they are getting started. How will they keep track of what they have tried?
Having had more time to work further on the challenge, the plenary could focus on the problem-solving skills they used to solve it. Most children will use trial and improvement and may strike lucky quite quickly. Listen for statements which give an indication that some logical thinking is going on - perhaps in terms of the biggest number a side could add to, or the smallest, or some
acknowledgement of the number of odds and evens which would affect the totals.
Key questions
How many dots are there altogether?
How many dots could there be on each side?
What is the largest total that is possible?
What is the smallest total that is possible?
Possible extension
Children could be asked to create an easier or a harder challenge, similar this one, and to explain what makes their task easier/harder than the original. You could collect the children's own problems and collate them into a book for the rest of the class/school to use.
Possible support
Children who are struggling can be asked to place the dominoes in any position and record the sums for each side. How many different totals can they find?
Which is the biggest? Why?
Which is the smallest? Why?