Isometric areas
Problem
Let's define a unit of area, $T$, such that the triangle has area $1T$.
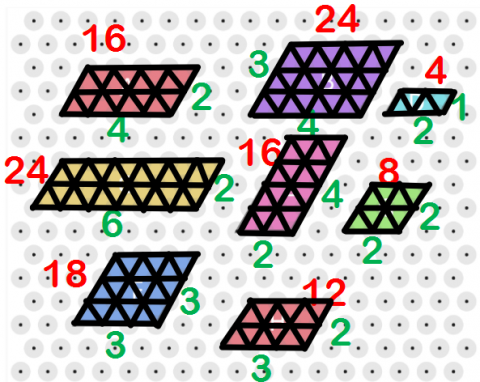
Here are some parallelograms whose side lengths are whole numbers.
Can you find the area, in terms of $T$, of each parallelogram?
Compare the results with the lengths of their edges.
What do you notice?
Can you explain what you've noticed?
Can you find a similar result for trapeziums in which all four lengths are whole numbers?
You might like to try More Isometric Areas next.
Getting Started
How many triangles are there in a parallelogram with side lengths
1 and 1?
2 and 1?
3 and 1?...
If you double one of the lengths, what would happen to the area?
If you double both of the lengths, what would happen to the area?
Student Solutions
A: 16 T
B: 24 T
C: 24 T
D: 4 T
E: 16 T
F: 18 T
G: 8 T
H: 12 T
This is the diagram that Matt from Swindon Academy in the UK used to show how triangles of area $1T$ can be drawn inside the parallelograms.
Clara from Bangkok Patana School in Thailand found the areas using larger triangles:
To find the area in $T$ units in all of the parallelograms you can simply count the amount of equilateral $T$ triangles in the shape. This however would take a long time so I realised that in a lot of the shapes there can fit a few of the same triangle just scale up by $4T$. I called these triangles '$t$' (lowercase).
Kannammai from West Island School in Hong Kong looked at the sides of the parallelograms in terms of 'bases' of the triangles with area $T$. This gives an insight into why the formula works.
Drawing in the 4 triangles whose bases make the top side (b), as shown below, notice that they don't overlap at all with the 2 triangles along side (a).
This means that inside the parallelogram are 4 sets of 2 triangles the same way around as those along side (a), and 2 rows of 4 triangles the same way round as those along side (b), giving a total of 2$\times$4+4$\times$2 = 16 triangles.
Aditya, Matt, Andre, Piyush, Swiss, Caitlin and Jemma explained the formula by thinking about units. Andre said:
b$\times$h$\times$2 = amount of '$T$s' in the parallelogram because b$\times$h = the amount of 'squares' in the parallelogram and because triangles have half the area of squares we need to multiply (b$\times$h) by 2.
Catilin said:
On isometric paper the units are "$T$", which are triangles. To get the area of a triangle you do b x h $\div$ 2, whereas for squares you simply do b $\times$ h. Therefore, because the units are "$T$" you would have to double the number of triangles as it is only half.
Finding the areas of Trapeziums
This is Matt's diagram for counting the triangles of area $T$ inside a trapezium.
Anna, Megha and Roshni from North London Collegiate School split the trapeziums into smaller shapes:
With trapeziums, the area is the same as any other parallelogram except you have to add the area of a triangle on to the area. The area of the triangle is also the area of the parallelogram. In this case, $9\times2=18$.
Matt, Caitlin, Swiss, Jemma, Ahan, Kannammai and Pavi, Sofia and Ayana found that the formula for the area of a trapezium in $T$ units is $(a+b)\times h$.
Jemma related this to the formula for the area of a trapezium in normal units:
This is because usually the formula would be ((Base A + Base B) x H) Divided by 2. However because the isometric triangle is half the normal square then you would times two and it would cancel the divided two out.
Pavi, Sofia and Ayana used a diagram to help explain why the formula works:
So as seen before, the sides of the parallelogram are equal to the height of the trapezium $h$ and the sum of the parallel sides, $a+b$. That means the area of the parallelogram is $2\times h\times(a+b)$ (from the working above), so the area of each trapezium must be $h\times (a+b)$.
Teachers' Resources
Why do this problem?
This problem invites students to look at area in a slightly different way from usual, using a triangle as the basic unit of area rather than a square, to reinforce the concept that area is about the space enclosed within a shape.
Along the way students have the opportunity to derive and justify a formula that they will not have met before.
Possible approach
Display an isometric dotty grid, and create a shape. This dotty grid environment might be useful, and you can print off isometric paper for students.
"On squared paper, it's easy to work out area by counting squares, but on isometric paper it's a bit different. If we want to compare areas of shapes drawn on isometric paper, we can use a small triangle as our unit of area, instead of a square!"
Create some simple shapes and work out the area as a class, perhaps inviting students to write their answers on mini whiteboards. Once everyone is confident at using the triangular unit of area, show students this slide with the image from the problem. "For each parallelogram, can you find its area, and then find a
relationship between the length of the sides of the parallelogram and its area, measured in triangular units?"
Give students some time to work in pairs on the problem, sharing any useful strategies and conjectures that they come up with. Then, once students begin to spot a relationship, invite them to consider why the relationship might occur and how they can justify it.
Students who finish quickly could be challenged to draw some trapeziums (in which all four lengths are whole numbers) and come up with a relationship between the side lengths and the area in triangular units.
Finish off by bringing the class together to share their justifications for the area rule they have found. A follow-up lesson could look at More Isometric Areas.
Key questions
How many triangles are there in a parallelogram with side lengths 1 and 1? 2 and 1? 3 and 1?...
If you double one of the lengths, what would happen to the area?
If you double both of the lengths, what would happen to the area?
Can you work out a formula for the area of parallelograms in triangular units?
Possible support
Torn Shapes works with areas based on counting squares, so would be a useful task for students who are not confident with area.
Possible extension
More Isometric Areas invites students to consider the area of triangles using triangular units.
Of All the Areas looks at the area of equilateral triangles with sides that are not whole numbers.