Right-angled midpoints
If the midpoints of the sides of a right angled triangle are joined, what is the perimeter of this new triangle?
Age
14 to 16
Challenge level
Problem
Image
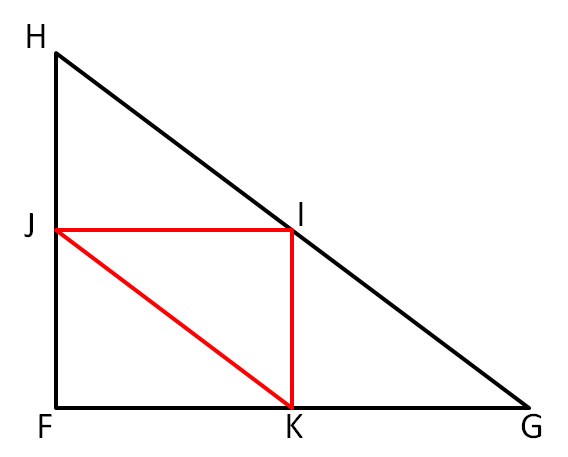
$I$, $J$, and $K$ are the mid points of the sides $GH$, $FH$ and $FG$ respectively.
What is the perimeter of the triangle $IJK$?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
Image
$GH = \sqrt{FH^2+FG^2} = \sqrt{6^2+8^2} = \sqrt{36+64} = \sqrt{100} = 10$
This means $FGH$ has perimeter $6+8+10 = 24\text{cm}$.
Consider the line $IJ$. The triangle $HIJ$ is similar to the triangle $HGF$. This is because $HJ = \frac 12 HF$, $HI = \frac 12 HG$ and $\angle JHI = \angle FHG$. This means $JI = \frac 12 FG = 4\text{cm}$.
Similarly, $JK = \frac 12 HG$ and $IK = \frac 12 FH$, so the perimeter of $IJK$ is half that of $FGH$. This means that $IJK$ has a perimeter of $12 \text{cm}$.