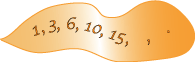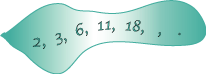Copyright © University of Cambridge. All rights reserved.
'The Mathemagician's Seven Spells' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem is a good one to do when the group is representing and interpreting different number patterns and sequences. The patterns grow successively harder, so that even those who might find the last ones difficult, should be able to start confidently on the problem.Possible approach
You could start by writing some different sequences on the board to introduce the problem.
These might be
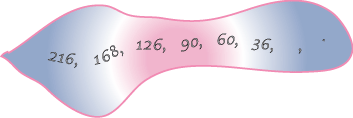
$1, 3, 5, 7, ...., ..... .$
$2, 7, 12, 17, ...., ..... .$
$1, 4, 9, 16, ...., ..... .$
$35, 29, 23, 17, ...., ..... .$
Learners could then work in pairs on the actual problem, perhaps from this sheet so that they are able to talk through their ideas with a partner. The hints give clues in the form of a continuation of the story should anyone become seriously stuck on one of the
sequences.
It would be a good idea to leave plenty of time to go through the sequences one by one, discussing how each pair of learners found the continuation of each of the sequences. There are many ways of finding the solutions. Listening to each others' explanations and putting their own into words should be a real learning experience. The last sequence is probably the most testing in this
respect!
You could finish off by giving the class the start of another sequence, for example: $1, 2, 4 ...$ and ask them to find as many different ways as they can to continue it, encouraging clear reasons for each answer. This is a valuable experience as it helps children understand that you can't always know from the first few numbers exactly how a sequence will continue.
Key questions
Have you seen a pattern of numbers like this before?
Have you seen these numbers together before?What is the gap between the first and second number?
What about between the second and the third?
Possible extension
Learners could extend some of the sequences and/or generate their own spells to puzzle their friends.Possible support
These hints may well prove helpful.