 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cycling Squares



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
William from Tattingstone School said that he tried four times before he came up with a solution to Cycling Squares:
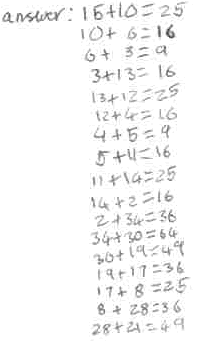
We're glad you didn't give up, William. Beth and Pheobe from Exminster CP School and Skye and Molly from Breckland Middle School also used trial and error (or trial and improvement as I like to call it!). Beth and Phoebe said it tested their skills of perseverance.
Matha, also from Tattingstone, said that she started with the number $2$ and then added $14$ because it was the only number she could have added to make a square number. She goes on to say:
I then added $11$ to $14$ to get $25$ which is another square number and carried on like this.
Martha sent in a drawing of her circle which is the same as William's answer, just written in a different way:
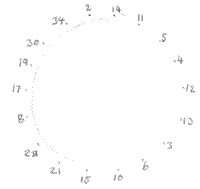
.
Dominic from Stonehill took a logical approach:
Brandon, Antonia and Oliver from Mayhill Junior used a similar method to Dominic. Emilie and Bethany from Alverstoke Junior School said:
Very well done to you all. Here are some comments we received in 2015 from pupils at Queen Edith, Cambridge having completed the challenge.
Edward:- "I worked it out by using trial and improvement and it took us a couple of times to figure it out. I started with one pair of numbers and went both ways around the circle"James:- "I worked out what numbers added together which would make a square number. Next we put two adjoining numbers to make a square number and we used trial and improvement to work out which number came next"
Lavinia:-" We worked together and persevered. If we got it wrong, we helped each other to make the answer right. Cooperating we completed the challenge even though it was hard!
Abigail :-"Clare and I chose the biggest number that was available in the range and made the first possible number that we could think of: 64 (30 + 34) We found out putting 34 first did not work so we put 30 first. We worked our way around the circle clockwise using trial and improvement to complete the challenge!
Lauren :-"Even though it was tricky we still persevered and tried our best. I had to use trial and improvement to make the circle but the best thing was to have fun!
Thank you Queen Edith pupils it made interesting reading. Well Done!