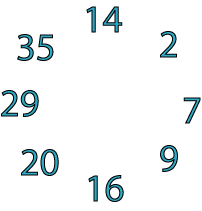Cycling Squares

'Cycling Squares' printed from https://nrich.maths.org/

Show menu

Cycling Squares

In the circle of numbers below each adjoining pair adds to make a square number:

circle of numbers from top going clockwise: 14, 2, 7, 9, 16, 20, 29, 35.

For example,

$14 + 2 = 16, 2 + 7 = 9, 7 + 9 = 16$

and so on.

Can you make a similar - but larger - cycle of pairs that each add to make a square number, using all the numbers in the box below, once and once only?

Numbers given: 2, 3, 4, 5, 6, 8, 10, 11, 12, 13, 14, 15, 7, 19, 21, 28, 30, 34

You might find it helpful to print off and cut up these cards of the numbers so you can move them around to try out your ideas.

Why do this problem?

This problem is a challenging one. It uses the learner's knowledge of square numbers and gives the opportunity of practising addition in an unusual context. It is a useful problem through which to discuss different methods of approach.

Possible approach

You could start by reminding the group about square numbers, perhaps by playing a game of 'I like ...' where you write up numbers you 'like' (i.e. are part of a set) to one side of the board and numbers you 'don't like' (i.e. are not in your set) to the other, as children suggest numbers. The idea is for children to determine the name of your set.

You could then use the small cycle given at the beginning of the problem to introduce the idea of a cycle of squares, encouraging learners to check that each pair of numbers does indeed add to a square number.

(The cycle goes like this: 14 - 2 - 7 - 9 - 16 - 20 - 29 - 35 -.)

Then you could go on to introducing the actual problem. Learners could work on this in pairs, using numbered counters that can be moved round experimentally or number cards printed from this sheet.

At the end of the lesson, all learners could be involved in a discussion of how they tackled the problem, building up the cycle on the board, number by number. You could invite them to comment about the advantages/disadvantages of the different methods used and they may decide that one method is particularly efficient.

Key questions

Can you think of a good way to start?

Have you made a list of square numbers up to 100?

Which of the numbers given can be added to that one to make a square number?

If you cannot go on from there, what could you try instead?

Possible extension

Learners could make their own cycle of squares using different numbers, or invent cycles using a different number property.

Possible support

Making a list of the square numbers up to 100 will help some children get started on this problem. Encourage the learner to choose one number and see which of the numbers given can be added to it to make a square number. Numbered counters to work with could be very helpful and a calculator might free-up some children who find calculation difficult.