The circle of Apollonius... coordinate edition

Thanks to Jordan from St Stephen's School, and Elin for submitting solutions to this problem.

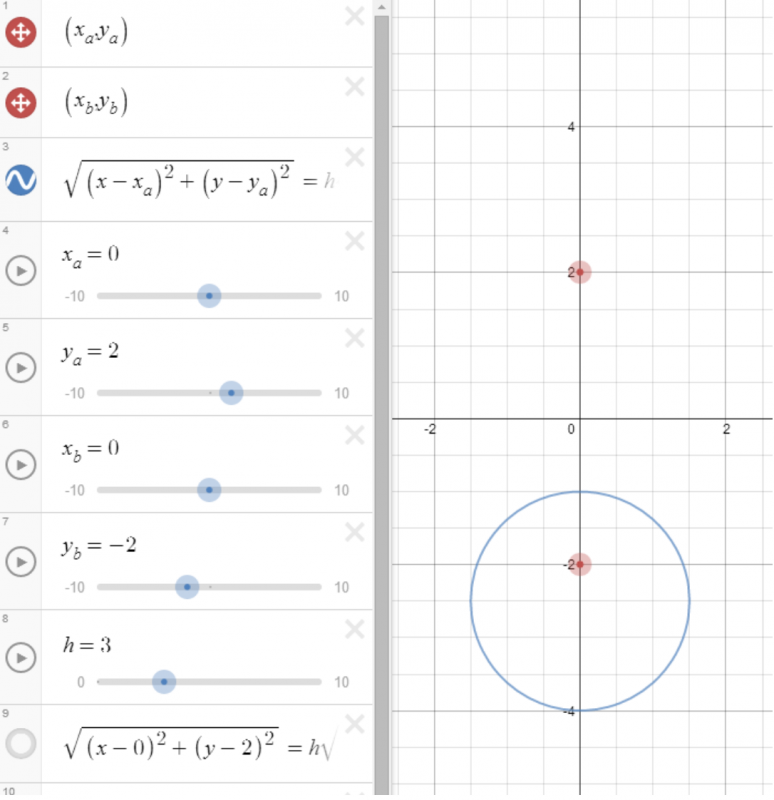
Jordan started off by using Desmos to plot the locus of P in various cases:

Assume $ \lambda=3 $ and $a=2$. Let A be the point $(0,2)$ and B be the point $(0,-2)$.

Then the equation for the locus of P can be written:

$$\sqrt{(x-0)^2+(y-2)^2}= 3 \sqrt{(x-0)^2+(y+2)^2}$$

When plotted in Desmos this gives a circle which looks like this:

 

Image

Desmos also allows the use of sliders so it is possible to explore different values of $\lambda$.

Below are plots for $\lambda=2$ and $\lambda=0.5$ in red:

 

Image

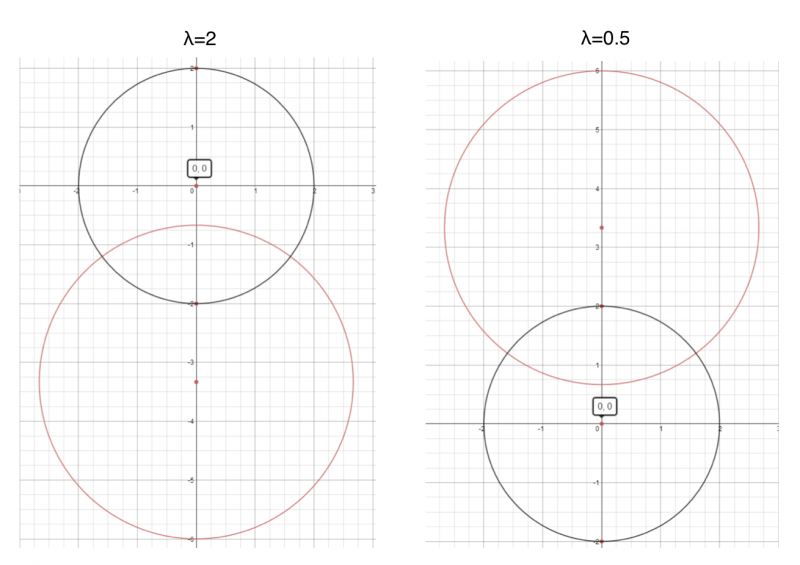
We observe that in both cases it gives a circle but when $\lambda=2$ the circle contains the point A and when $\lambda=0.5$ the circle contatins the point B.

In Elin's solution she has rearranged the equation for the locus of P so that it is in the standard form of the equation of a circle:

Let A be the point $(0,0)$ and B be the point $(0,4)$.

(It doesn't matter that Elin has used different points A and B to Jordan, all that matters is that the distance between A and B is 4. It does however mean that Elin's initial equation is slightly different, but it is arrived at in the same way)

Then the equation of the locus of P is:

$\sqrt{(x-0)^2+(y-0)^2}= 3 \sqrt{(x-4)^2+(y-0)^2}$

$x^2+y^2= 9((x-4)^2+y^2)$

$x^2+y^2= 9(x^2-8x+16+y^2)$

$x^2+y^2= 9x^2-72x+144+9y^2$

$ 8x^2-72x+144+8y^2=0$

$ x^2-9x+18+y^2=0$

$ (x-9/2)^2-9/2^2+18+y^2=0$

$ (x-9/2)^2+y^2=9/2^2-18$

$ (x-9/2)^2+y^2=9/4$

Hence the locus of P is a circle with centre $(\frac{9}{2},0)$ and radius $\frac{3}{2}$.

Elin has also done the same in the general case where $a$ and $\lambda$ are not fixed

Let A be the point $(0,0)$ and B be the point $(0,2a)$.

Then the equation of the locus of P is:

$\sqrt{(x-0)^2+(y-0)^2}= \lambda \sqrt{(x-2a)^2+(y-0)^2}$

$x^2+y^2= \lambda^2((x-2a)^2+y^2)$

$x^2+y^2= \lambda^2(x^2-4ax+4a^2+y^2)$

$x^2+y^2= \lambda^2 x^2-4a\lambda^2 x+4a^2\lambda^2+\lambda^2 y^2$

$ (\lambda^2-1)x^2-4a\lambda^2 x+4a^2\lambda^2+(\lambda^2-1)y^2=0$

$ x^2-\frac{4a\lambda^2}{\lambda^2-1}x+\frac{4a^2\lambda^2}{\lambda^2-1}+y^2=0$

$ (x-\frac{2a\lambda^2}{\lambda^2-1})^2-(\frac{2a\lambda^2}{\lambda^2-1})^2+\frac{4a^2\lambda^2}{\lambda^2-1}+y^2=0$

$(x-\frac{2a\lambda^2}{\lambda^2-1})^2+y^2=(\frac{2a\lambda^2}{\lambda^2-1})^2-\frac{4a^2\lambda^2}{\lambda^2-1}$

$(x-\frac{2a\lambda^2}{\lambda^2-1})^2+y^2=\frac{4a^2\lambda^2}{(\lambda^2-1)^2}$

$(x-\frac{2a\lambda^2}{\lambda^2-1})^2+y^2=(\frac{2a\lambda}{\lambda^2-1})^2$

Hence the locus of P is a circle with centre $(\frac{2a\lambda^2}{\lambda^2-1},0)$ and radius $\frac{2a\lambda}{|\lambda^2-1|}$.

In fact, there is one value of $\lambda$, $\lambda=1$, where the locus isn't a circle - it is a straight line which is the bisector of AB, because in this case the distance from P to A is the same as the distance from P to B. Can you see where in the working above we needed the fact that $\lambda$ was not equal to 1, in order to get the equation of a circle?

For the second part of the question, Jordan noticed that since the tangent from the midpoint of AB to the circle will be perpendicular to the radius of the circle, the length of the tangent to this circle from the mid-point of AB can be calculated using Pythagoras:

In the case where $a=2$, $\lambda=3$, the radius of the circle is 3/2 and the distance between the midpoint of AB and the centre of the circle is 5/2 so by Pythagoras' theorem the length of the tangent is

$$\sqrt{(5/2)^2-(3/2)^2}=2$$

This is the same as half the distance between A and B, so the circle centred on the midpoint of AB with radius 2 will intersect the original circle in the tangential point. This is illustrated below:

 

Image

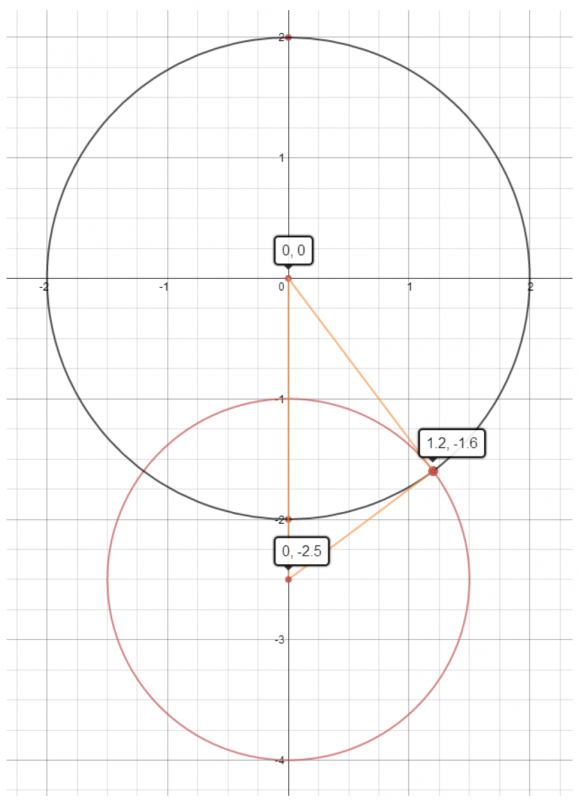
This distance turns out to be the same whatever the value of $\lambda$, so the tangential point always lies on the circle with centre the midpoint of AB and radius 2.

The shape traced by the tangential point for values of $\lambda <1$ is the half of the circle closest to A and for values of $\lambda>1$ is the half of the circle closest to B as illustrated below:

 

Image

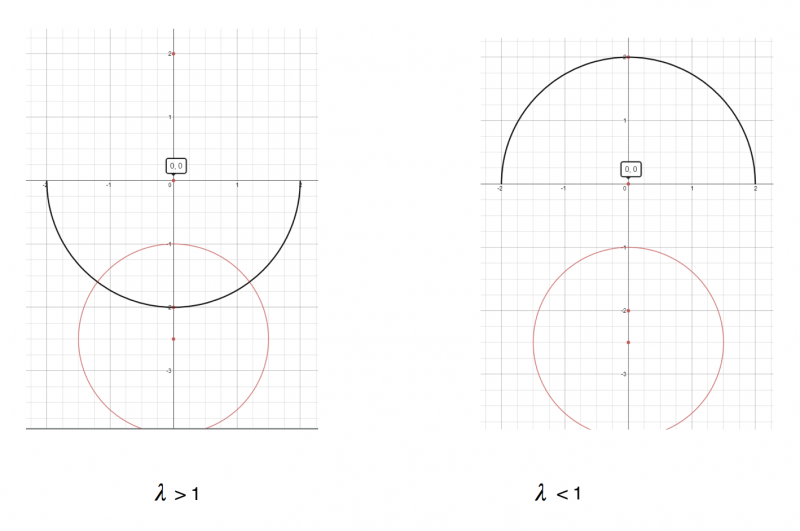
Elin has proved these observations in the general case where $a$ and $\lambda$ are not fixed:

Let M be the mid point of AB, C be the centre of the circle which is the locus of P, and T be the tangential point.

Then

$MC=\frac{2a\lambda^2}{\lambda^2-1}-a$

$CT=\frac{2a\lambda}{|\lambda^2-1|}$

Since MTC is a right angled triangle we can work out the length MT by Pythagoras:

$MT^2=MC^2-CT^2$

$=(\frac{2a\lambda^2-a(\lambda^2-1}{\lambda^2-1})^2-(\frac{2a\lambda}{|\lambda^2-1|})^2$

$=(\frac{a(\lambda^2+1)}{\lambda^2-1})^2-(\frac{2a\lambda}{|\lambda^2-1|})^2$

$=(\frac{(a(\lambda^2+1))^2-(2a\lambda)^2}{(\lambda^2-1)^2})$

$=(\frac{a^2(\lambda^4+2\lambda^2+1)-4a^2\lambda^2}{(\lambda^2-1)^2})$

$=(\frac{a^2(\lambda^4-2\lambda^2+1)}{(\lambda^2-1)^2})$

$=(\frac{a(\lambda^2-1)^2}{(\lambda^2-1)})^2$

$=a^2$

In conclusion $MT=a$, which in words says that the length of the tangent is $a$, whatever the value of $\lambda$ is, so the tangential point lies on a circle with centre the midpoint of AB, and radius $a$.