Back to the planet of Vuvv
There are two forms of counting on Vuvv - Zios count in base 3 and Zepts count in base 7. Can you work out in which direction the Zios and Zepts were looking, based on the information you're given?
Problem
On the planet Vuvv there are two sorts of creatures. The Zios have $3$ legs and the Zepts have $7$ legs.
So naturally there are two forms of counting on Vuvv - Zios count in base $3$ and Zepts count in base $7$.
When observed, the creatures on this planet lie on the ground with their legs in the air, so that legs, not bodies, can be most easily counted.
One day four of these creatures, two Zios and two Zepts, sat on the summit of a hill to count the legs of the creatures they could see. One looked to the East, one to the West, one to the South and one to the North.
The creature looking to the West wrote down its number: $122$
The creature looking to the East wrote down its number: $22$
The creature looking to the South wrote down its number: $101$
The creature looking to the North wrote down its number: $41$
In which direction are the two Zios looking and in which directions are the two Zepts looking?
Getting Started
Numbers are written by arranging digits in a row and each place in the row has a different value. This value depends on the base of the number system. The most common base nowadays is 10:
| 10x10x10x10 | 10x10x10 | 10x10 | 10 | 1 |
| Ten thousands | Thousands | Hundreds | Tens | Units/Ones |
We often use these short forms for the columns:
| TTh | Th | H | T | U |
To count in different bases, we just group numbers in a different way. For example, for base 2:
| 2x2x2x2x2x2 | 2x2x2x2x2 | 2x2x2x2 | 2x2x2 | 2x2 | 2 | 1 |
| Sixty fours | Thirty twos | Sixteens | Eights | Fours | Twos | Units/Ones |
Zios count in base 3 so their numbers are grouped like this (we shall only look at the first three columns):
| 3x3 | 3 | 1 |
| Nines | Threes | Units/Ones |
Let's work out what a Zio's 111 is in human numbers (base 10):
| Nines | Threes | Units/Ones |
| 1 | 1 | 1 |
So, 111 = (1 x 9) + (1 x 3) + 1 = 13.
Zepts count in base 7 so their numbers are grouped like this:
| 7x7 | 7 | 1 |
| Forty nines | Sevens | Units/Ones |
Let's see what a Zept's 111 is in base 10:
| Forty nines | Sevens | Units/Ones |
| 1 | 1 | 1 |
So, 111 = (1 x 49) + (1 x 7) + 1 = 57.
To find out which way each type of creature is facing, calculate each number in human counting (base 10).
Remember that the creatures must be seeing numbers which could be a combination of Zios' and Zepts' legs.
Student Solutions
Martha in Year 5 at Hatherleigh Primary School has sent us a very well explained solution to this tricky problem. She says:
First I counted up to $122$ in base $3$ and base $7$. Then I marked them off in fives in base $10$.
Here is her working:

She goes on to say:
After that I wrote down the four numbers we were given, found out what they were in base $3$ and $7$, and worked out whether or not they could be made out of $7$s and $3$s:
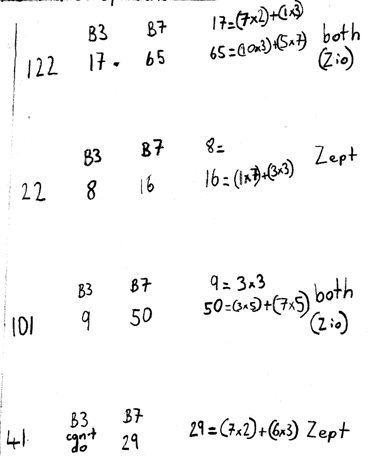
N.B. There's a slight error above: 101 in Base 3 is equivalent to 10 in Base 10, not 9, so could be the total number of legs of one Zio and one Zept.
$22$ and $41$ could only be in base $7$ so the other two were Zios. So:
West - Zio
East - Zept
South - Zio
North - Zept
Excellent Martha - thank you for sharing your answer with us.
Teachers' Resources
Why do this problem?
Key questions
Possible extension
Learners could make a similar puzzle for themselves, or go on to this similar problem: Basically.
Possible support
Suggest trying Alien Counting instead which is a simpler problem of the same type.
