Copyright © University of Cambridge. All rights reserved.
'Early Number Sense' printed from https://nrich.maths.org/
Show menu
This article explores the basic foundations of number sense and outlines relevant research in this area. It updates Jenni Way's article Number Sense Series: Developing Early Number Sense.
What is number sense?
The term "number sense" was coined in the late 80s and early 90s and gained currency during the early days of the National Curriculum as something that we hoped children would achieve by the end of their primary schooling. In Jenni Way's original article (2001), Bobis' definition is highlighted, suggesting that it referred to "a well organised conceptual framework of number
information that enables a person to understand numbers and number relationships and to solve mathematical problems that are not bound by traditional algorithms" (Bobis, 1996). Over the last few years in conjunction with my research work in Hungary and the attendant comparative work that I have been engaging in with Judy Sayers and Paul Andrews, I have been exploring some more recent
developments in the research into this area.
What does the research tell us?
The research into the development of number sense is divided into two camps. The first of these is concerned with the development of number sense in young children whereas the second is focused on the number sense that people require to function well in the world. In the context of this article, I will limit my consideration to the work on number sense and its development in young children.
In this context, no two researchers in the field accept the same definition but a trawl of recent research yielded a number of common elements and Paul, Judy and I (Andrews, Sayers and Back, 2013) summarised seven common threads that were evident in studies drawn from a number of different cultures. These
were:
1. An awareness of the relationship between number and quantity
2. An understanding of number symbols, vocabulary and meaning
3. The ability to engage in systematic counting, including notions of cardinality and ordinality
4. An awareness of magnitude and comparisons between different magnitudes
5. An understanding of different representations of number
6. Competence with simple mathematical operations
7. An awareness of number patterns including recognising missing numbers
These seven ideas seem to capture the essence of what is being referred to as 'number sense'.
Having developed ideas of the concept from research, how can we, as teachers, help to support its development in our learners? There is no doubt that it is not something that children have innately but rather something which they can develop over time. As Sood and Jitendra (2007) say:
For me the ways in which it can be supported need to be based on giving learners opportunities to make sense of, and reason about, number. They will need to be given reasons to communicate their ideas about arithmetic; to develop fluent recall of key facts and be able to apply them to novel contexts; to have easy access to a range of appropriate and useful representations; to be able to apply
ideas to new concepts and to solving problems.
What teaching strategies promote early number sense?
A number of strategies that help to support developing number sense are described by Tsao and Lin (2012). They suggest that children need opportunities to:
1. Work with concrete materials and familiar ideas
2. Compose and recompose different arrangements and representations of number
3. Discuss and share their discoveries and solutions
4. Investigate the realistic uses of number in their everyday world
5. Explore number patterns and relationships
6. Create alternative methods of calculation and estimation
7. Solve realistic problems using a variety of approaches
8. Calculate for a purpose rather than just for the sake of calculating
9. Gather, organise, display and interpret quantitative data
10. Measure and estimate measure for a purpose
11. Explore very large numbers and their representations including using number lines
Quite a list! Yet if we really thought about every aspect of these opportunities in relation to every incremental step on the way to the development of number sense, there is no doubt that our learners would develop deeper and richer understandings of number. In the space of this article, I should like to draw your attention to the key ones that are particularly relevant to supporting young
children in developing their understanding of numbers under twenty and especially numbers under ten.
1. Work with concrete materials and familiar ideas
To begin with, early number activities are best done with moveable objects such as counters, blocks and small toys. Most children will need the concrete experience of physically manipulating groups of objects into sub-groups and combining small groups to make a larger group. After these essential experiences more static materials such as 'dot cards' become very useful.
2. Compose and recompose different arrangements and representations of number
By simply presenting objects (such as collections of concrete objects, stamps on a flashcard, buttons sewn onto a card, Rawlplugs in linked groups and so on) in various arrangements, different mental strategies can be prompted. For example, showing six stamps in a cluster of four and a pair prompts the combination of 'four and two makes six'. If the four is not subitised, it may be seen as 'two
and two and two makes six'. This arrangement is obviously a little more complex than two groups of three. So different arrangements will prompt different strategies, and these strategies will vary from person to person, from learner to learner. Asking children to find all the dominoes in a six spot set with 6 spots on will encourage them to consider all the ways in which 6 can be partitioned into
two sets and build up their understanding of the number bonds for six.
3. Discuss and share their discoveries and solutions
If mental strategies such as these are to be encouraged (and counting discouraged) then an element of speed is necessary. Seeing the objects for only a few seconds challenges the mind to find strategies other than counting. It is also important to have children reflect on and share their strategies. This is helpful in three ways:
- verbalising a strategy brings the strategy to a conscious level and allows the person to learn about their own thinking;
- it provides other children with the opportunity to pick up new strategies;
- the teacher can assess the type of thinking being used and adjust the type of arrangement, level of difficulty or speed of presentation accordingly.
Dot cards are simply cards with dot stickers of a single colour stuck on one side. (However, any markings can be used. Self-inking stamps are fast when making a lot of cards). The important factors in the design of the cards are the number of dots and the arrangement of these dots. The various combinations of these factors determine the mathematical structure of each card, and hence the types
of number relations and mental strategies prompted by them.
Consider each of the following arrangements of dots before reading further. What mental strategies are likely to be prompted by each card? What order would you place them in according to level of difficulty?
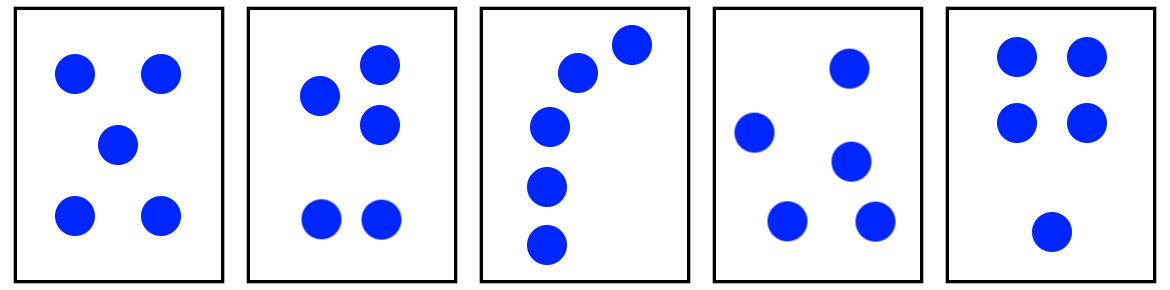
A B C D E
Card A is the classic symmetrical dice and playing card arrangement of five and so is often instantly recognised without engaging other mental strategies. It is perhaps the easiest arrangement of five to deal with.
Card B presents clear sub-groups of two and three, each of which can be instantly recognised. With practice, the number fact of 'two and three makes five' can be recalled almost instantly.
Card C: A linear arrangement is the one most likely to prompt counting. However, many people will mentally separate the dots into groups of two and three, as in the previous card. Other strategies such as seeing two then counting '3, 4, 5' might also be used.
Card D could be called a random arrangement, though in reality it has been quite deliberately organised to prompt the mental activity of sub-grouping. There are a variety of ways to form the sub-groups, with no prompt in any particular direction, so this card could be considered to be the most difficult one in the set.
Card E shows another sub-group arrangement that encourages the use (or discovery) of the 'four and one makes five' number relation.
Obviously, using fewer than five dots would develop the most basic number sense skills, and using more than five dots would provide opportunities for more advanced strategies. However, it is probably not useful to use more than ten dots. (See this linked article of developing a 'sense of ten' and 'place value readiness'). Cards such as these can be shown briefly to children, then the children can
be asked how many dots they saw. The children should be asked to explain how they perceived the arrangement, and hence what strategies they used.
4. Investigate the realistic uses of number in their everyday world
In my Hungarian research I followed the mathematical development of a class of children through the first years of their formal schooling and was particularly struck by the careful grounding they were given in the foundations of arithmetic. When they started school one week was devoted to each of the numbers under ten in turn and they looked for examples of it in their everyday world as well in
the classroom and school context. So for the number 3 they would have looked for items that had aspects of 3 associated with them such as tricycles or three legged stools. They would have explored stories with three in them such as Goldilocks and the Three Bears, the Billy Goats Gruff or the Three Little Pigs. They would have talked about those who were in families with three children in them,
those who had three siblings or families with three in the house. They would have explored children aged three years and buses and houses with the number 3. Coming third in a queue or a race would have been connected to the notion and they would have made a special point of considering things that happen at 3 o'clock. This deep and thorough investigation of numbers seems to support the children's
developing sense of the number and we could gain from building it into the experiences we offer our young learners.
Where do I go from here?
The article Place Value: The Ten-ness of Ten follows on from this one. It outlines how having a strong 'sense of ten' lays foundations for understanding place value and carrying out mental calculations. For activities to try in the classroom, see our article How Can I Support the Development of Early Number Sense and Place Value? as well
as our Number Sense and Place Value Feature.
References
Andrews, P., Sayers, J. & Back, J. (2013) The development of foundational number sense in England and Hungary: a case study comparison. Conference Proceedings: CERME 2013.
Bobis, J. (1996). Visualisation and the development of number sense with kindergarten children. In Mulligan, J. & Mitchelmore, M. (Eds.) Children's Number Learning : A Research Monograph of the Mathematics Education Group of Australasia and the Australian Association of Mathematics Teachers. Adelaide: AAMT.
Gelman, R. & Gallistel, C. (1978). The Child's Understanding of Number. Cambridge, MA: Harvard University Press.
Sood, S., & Jitendra, A. K. (2007). A Comparative Analysis of Number Sense
Instruction in Reform-Based and Traditional Mathematics Textbooks. Journal of
Special Education, 41(3), 145-157.
Tsao, Y.L. & Lin, Y. C. (2012) Elementary School Teachers' Understanding: Towards the Related Knowledge of Number Sense. US - China Education Review B1. (p 17 - 30) davidpublishing.com.
Here is a PDF version of this article.