Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Resources tagged with: Calculators
There are 5 results
Broad Topics > Physical and digital manipulatives > Calculators
Problem
Primary curriculum
Secondary curriculum

Dating Made Easier
If a sum invested gains 10% each year how long before it has doubled its value?
Age 14 to 16
Challenge Level 





Problem
Primary curriculum
Secondary curriculum

Climbing Powers
$2\wedge 3\wedge 4$ could be $(2^3)^4$ or $2^{(3^4)}$. Does it make any difference? For both definitions, which is bigger: $r\wedge r\wedge r\wedge r\dots$ where the powers of $r$ go on for ever, or $(r^r)^r$, where $r$ is $\sqrt{2}$?
Age 16 to 18
Challenge Level 





Problem
Primary curriculum
Secondary curriculum

Rain or Shine
Predict future weather using the probability that tomorrow is wet given today is wet and the probability that tomorrow is wet given that today is dry.
Age 16 to 18
Challenge Level 





Article
Primary curriculum
Secondary curriculum

Adding with the Abacus
Nowadays the calculator is very familiar to many of us. What did people do to save time working out more difficult problems before the calculator existed?
Age 5 to 16
Problem
Primary curriculum
Secondary curriculum
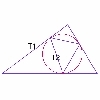
Triangle Incircle Iteration
Keep constructing triangles in the incircle of the previous triangle. What happens?
Age 14 to 16
Challenge Level 




