Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Resources tagged with: Complex numbers
There are 6 results
Broad Topics > Place value and the number system > Complex numbers
Problem
Primary curriculum
Secondary curriculum
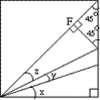
8 Methods for Three by One
This problem in geometry has been solved in no less than EIGHT ways by a pair of students. How would you solve it? How many of their solutions can you follow? How are they the same or different? Which do you like best?
Age 14 to 18
Challenge Level 





List
Primary curriculum
Secondary curriculum

Adventures with Complex Numbers
This collection is designed to give an introductory taste of complex numbers.
Age 14 to 18
Challenge Level 





Problem
Primary curriculum
Secondary curriculum

Strolling Along
What happens when we multiply a complex number by a real or an imaginary number?
Age 14 to 18
Challenge Level 





Article
Primary curriculum
Secondary curriculum

What Are Numbers?
Ranging from kindergarten mathematics to the fringe of research this informal article paints the big picture of number in a non technical way suitable for primary teachers and older students.
Age 7 to 18
Problem
Primary curriculum
Secondary curriculum

Napoleon's Theorem
Triangle ABC has equilateral triangles drawn on its edges. Points P, Q and R are the centres of the equilateral triangles. What can you prove about the triangle PQR?
Age 14 to 18
Challenge Level 




