Penny, Tom and Matthew were each given a box of mint chocolates
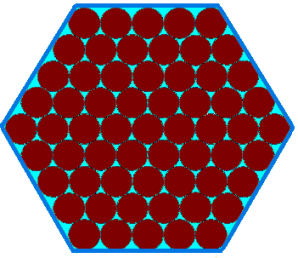
in a hexagonal box:
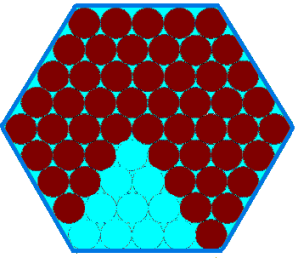
Penny ate $10$ chocolates:
When she looked at the remaining chocolates, she quickly
worked out that there must have been $61$ chocolates at the
start.
Tom ate $20$ chocolates:
He also managed to work out very quickly that there were
originally $61$ chocolates.
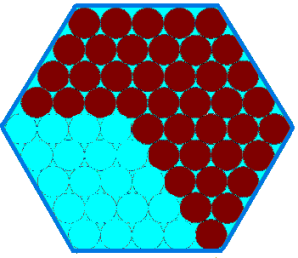
Matthew ate $24$ chocolates:
He could also see very easily that he must have started with
$61$ chocolates.
Penny, Tom and Matthew have been promised a larger box of
chocolates as a Christmas present from their grandmother. The
box will have $10$ chocolates along each edge, instead of
just $5$.
How would each child work out how many chocolates the larger
box will contain?
Can you describe any other ways to work it out?
Here are some more questions you might like to consider:
- For which sizes of chocolate
box will the three children be able to share the chocolates
equally?
- For which sizes of chocolate
box will the boys be able to share the chocolates
equally?
- Can you describe how each child
would work out the number of chocolates in a box with $n$
chocolates along each edge?