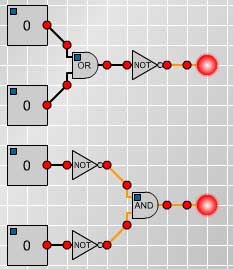
In this article you will find explanations of circuits and how they correspond to the logical language we use to discuss mathematics. You will be challenged to summarise the workings of the circuits by filling in blanks in the corresponding truth tables. To check your answers you can then switch to another version of this article which has all the truth tables complete. This diagram gives a summary of the information you will need to build your own circuits.

Although logic does not model language perfectly it does form a useful system that, in practice, is the basis of most of the communication of mathematical ideas between working mathematicians. Logical conventions are used to overcome the ambiguities and inadequacies of language. The philosophical aspects of the subject are rather more subtle and complicated and we shall not dwell on them.

A proposition is a statement that has exactly one of the truth values 'true' or 'false'. A propositional function is a sentence involving variables, for example "She is the Queen of England" and "x is greater than 7". These functions become propositions when meanings are substituted for the variables ('she' and 'x' in the above examples).

Before we go on to experiment with circuits we need a notation to record and summarize the combinations of propositions used in logical arguments and also the combinations of switches used in circuits.

We use small letters $p,q,r...$ to represent propositions. If the proposition $p$ is true it is said to have the truth value 1 (or sometimes T) and if false the truth value 0 (or F). Propositional logic is concerned with compound propositions formed from given propositions by means of the connectives 'not', 'and', 'or', 'if ... then' and combinations of these connectives, for example 'if and only if'.

In circuit diagrams each switch is either 'on' (representing the number 1) or 'off' (representing the number 0). Combinations of switches called logical gates represent the logical connectives.

Logical arguments are a combination of propositions, and circuits are a combination of switches that control the flow of current. Modern computers not only store data in the form of '0's and '1's, on which they perform arithmetic, but perform many highly complex tasks that we have come to take for granted. Studying the relation between truth tables and circuits will help us to understand a little of the underlying principles behind the design and programming of computers.

Negation

Now it is time to use Circuit Maker to make some of your own circuits and find out how the logic gates work.

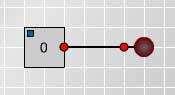
First, connect a switch to a lamp as in Fig. 1 and click on the switch several times to change it from 1 to 0 and back to 1. Observe that the light goes on when the switch registers 1 and the light goes off when the switch registers 0.

Fig. 1

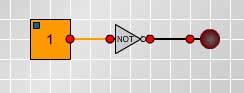
Fig. 2

Now put a NOT gate into the circuit between the switch and the lamp, as shown in Fig. 2, and observe what happens when you change the switch from 1 to 0.

Given a proposition $p$, the negation not- $p$, written $\neg p$, is the proposition demonstrated by this circuit and defined by the following truth table.

${\displaystyle \begin{array}{cc}\hfill p\hfill & \hfill \neg p\hfill \\ \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}}$

Conjunction

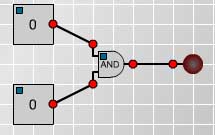
The logical connective 'and' is used to make a compound proposition from two component propositions. For example if we speak the truth when we say "Today is Friday and it is raining" then both of the component propositions are true. If either or both are false then the compound proposition is false.

Make and test the circuit shown in Fig 3. and fill in the truth table replacing the question marks with 1's to record when the lamp lights up and 0's to record when the lamp goes off.

Fig. 3

${\displaystyle \begin{array}{ccc}\hfill p\hfill & \hfill q\hfill & p\wedge q\\ \hfill 1\hfill & \hfill 1\hfill & ?\\ \hfill 1\hfill & \hfill 0\hfill & ?\\ \hfill 0\hfill & \hfill 1\hfill & ?\\ \hfill 0\hfill & \hfill 0\hfill & ?\end{array}}$

If you want to check your work then you can click here to get the article with all the blanks filled in.

Disjunction

In everyday language we often use 'or' inclusively as in Ïf you want to buy cereals or soft drinks go to aisle 7 in the supermarket" when we expect people who want to buy both cereals and soft drinks to go to that aisle as well as people wanting to buy just one of them. On other occasions we use 'or' exclusively to offer two alternatives expecting the listener to choose just one of them as in "Do you want steak for dinner or chicken?". The meaning is usually clear from the context but to avoid any ambiguity in mathematics the logical connective 'or' is always used inclusively and never exclusively.

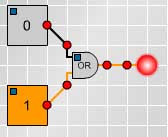
Given any two propositions $p$ and $q$ the disjunction $p$ or $q$, (written $p\vee q$)is given in the following truth table.

Fig.4

Make the circuit shown in Fig 4. and fill in the blanks in the truth table replacing the question marks with 1's and 0's..

${\displaystyle \begin{array}{ccc}\hfill p\hfill & \hfill q\hfill & p\vee q\\ \hfill 1\hfill & \hfill 1\hfill & ?\\ \hfill 1\hfill & \hfill 0\hfill & ?\\ \hfill 0\hfill & \hfill 1\hfill & ?\\ \hfill 0\hfill & \hfill 0\hfill & ?\end{array}}$

Compound propositions

Truth tables for more complicated compound propositions can be formed from the simpler ones. For example, the following truth table and circuit (Fig 5) show that $\neg (p\vee q)$ has the same truth values as $\neg p\wedge \neg q$. Make the circuit and fill in the missing values in the truth table.

Fig. 5

${\displaystyle \begin{array}{ccccccc}\hfill p\hfill & \hfill q\hfill & p\vee q& \neg (p\vee q)& \neg p& \neg q& \neg p\wedge \neg q\\ \hfill 1\hfill & \hfill 1\hfill & 1& ?& 0& 0& ?\\ \hfill 1\hfill & \hfill 0\hfill & 1& ?& 0& 1& ?\\ \hfill 0\hfill & \hfill 1\hfill & 1& ?& 1& 0& ?\\ \hfill 0\hfill & \hfill 0\hfill & 0& ?& 1& 1& ?\end{array}}$

XOR, NAND, NOR and XNOR

Next we investigate some of the other logical gates used in circuitry. Then we shall discuss other important logical connectives such as 'implies', often expressed as 'if... then' as in " if I go to the shops then I'll buy you some ice-cream". After that we shall be able to relate the circuits to the language of logical arguments and also see how circuits can be built to perform simple operations such as addition.

Now experiment with the circuits for XOR, NAND, NOR and XNOR and complete the following truth table replacing the question marks with 1's and 0's.

${\displaystyle \begin{array}{cccccc}\hfill p\hfill & \hfill q\hfill & p\mathrm{XOR}q& p\mathrm{NAND}q& p\mathrm{NOR}q& p\mathrm{XNOR}q\\ \hfill 1\hfill & \hfill 1\hfill & ?& ?& ?& ?\\ \hfill 1\hfill & \hfill 0\hfill & ?& ?& ?& ?\\ \hfill 0\hfill & \hfill 1\hfill & ?& ?& ?& ?\\ \hfill 0\hfill & \hfill 0\hfill & ?& ?& ?& ?\end{array}}$

Comparing these tables to what we have already discovered we see that p NOR q means 'not(p or q)', that is $\neg (p\vee q)$, and it is also equivalent to $\neg p\wedge \neg q$.

Also p NAND q means 'not(p and q)', that is $\neg (p\wedge q)$, and it is also equivalent to $\neg p\vee \neg q$.

Thinking about what we mean by 'if p then q' we see that this rules out the possibility that p is true and q is false. If I make the promise " if I go to the shops then I'll buy you some ice-cream" but I go to the shop and do not buy the ice-cream then I have broken my promise. So, denoting 'if p then q' by $p\Rightarrow q$, the truth table for 'if p then q' must include the line:

${\displaystyle \begin{array}{ccc}\hfill p\hfill & \hfill q\hfill & p\Rightarrow q\\ \hfill 1\hfill & \hfill 0\hfill & 0\end{array}}$

As the following example shows true conclusions can be proved by valid arguments from false premises and so we should expect 'false $\Rightarrow$ true' to be true.

We shall prove the proposition '2=1 $\Rightarrow$ 2=2'. Of course 2=2 is true (by definition) but the following argument proves this as a consequence of a false hypothesis.

By the symmetry of equality if 2=1 then 1=2. By the transitivity of equality it follows that, having shown 2=1 and 1 = 2, then 2 = 2.

This establishes a second line in the truth table for implication.

${\displaystyle \begin{array}{ccc}\hfill p\hfill & \hfill q\hfill & p\Rightarrow q\\ \hfill 1\hfill & \hfill 0\hfill & 0\\ \hfill 0\hfill & \hfill 1\hfill & 1\end{array}}$

There might still be some doubt in the reader's mind about why the definition of 'false' implies 'true' is 'true'. It could not be false because then we would have $p\Rightarrow q$ logically the same as $q\Rightarrow p$ which is not the case. Consider for example $x=1\Rightarrow x>0$ which is true whereas $x>0\Rightarrow x=1$ is false, so we have no choice but to make this definition for $p\Rightarrow q$.

Also 'if x then x' is true whether x is true or false so we must have the complete truth table as follows.

${\displaystyle \begin{array}{ccc}\hfill p\hfill & \hfill q\hfill & p\Rightarrow q\\ \hfill 1\hfill & \hfill 1\hfill & 1\\ \hfill 1\hfill & \hfill 0\hfill & 0\\ \hfill 0\hfill & \hfill 1\hfill & 1\\ \hfill 0\hfill & \hfill 0\hfill & 1\end{array}}$

It is convenient to have a single connective which combines $p\Rightarrow q$ and $q\Rightarrow p$. This connective is the bi-conditional 'p if and only if q' (written $p\iff q$)and defined by the truth table:

${\displaystyle \begin{array}{ccc}\hfill p\hfill & \hfill q\hfill & p\iff q\\ \hfill 1\hfill & \hfill 1\hfill & 1\\ \hfill 1\hfill & \hfill 0\hfill & 0\\ \hfill 0\hfill & \hfill 1\hfill & 0\\ \hfill 0\hfill & \hfill 0\hfill & 1\end{array}}$

We observe that in the truth table for $p\iff q$ this compound proposition is true precisely in those circumstances in which p and q have the same truth values and this is given by the logic gate p XNOR q. Also observe that the logic gate p XOR q is equivalent to $\neg (p\iff q)$.

Note that p XOR q is 'the exclusive or', true when either p is true or when q is true but not when they are both true. In everyday language we often use the exclusive or, as in "do you want steak or chicken for dinner?", but to the mathematician who, by convention, uses only the inclusive or, the logical answer is " yes" if he wants meat for dinner and "no" if he does not want meat.

Tautologies

If the truth value of a compound proposition is always true for all possible combinations of truth values of the given propositions, then the compound proposition is called a tautology. The following truth table and circuit show that $p\vee \neg p$ is a tautology. This is called the Law of the Excluded Middle because either $p$ is true or $\neg p$ is true and there is no third alternative.

Fig. 7

${\displaystyle \begin{array}{ccc}\hfill p\hfill & \hfill \neg p\hfill & p\vee \neg p\\ \hfill 1\hfill & \hfill 0\hfill & 1\\ \hfill 0\hfill & \hfill 1\hfill & 1\end{array}}$

The Sheffer stroke

The five connectives $\neg ,\wedge ,\vee ,\Rightarrow ,\iff$ can be defined by one symbol called the Sheffer stroke which was devised by H.M.Sheffer in 1913. At the time it was simply a piece of pure mathematics, but later it has had applications in designing electronic circuits from assemblies of a single component, the NAND gate. We have already seen that p NAND q is equivalent to 'not p or not q' or, equivalently, 'not (p and q)' and that it has the following truth table.

${\displaystyle \begin{array}{ccc}\hfill p\hfill & \hfill q\hfill & p\mathrm{NAND}q\\ \hfill \hfill & \hfill \hfill & \mathrm{Sheffer}\mathrm{stroke}\\ \hfill 1\hfill & \hfill 1\hfill & 0\\ \hfill 1\hfill & \hfill 0\hfill & 1\\ \hfill 0\hfill & \hfill 1\hfill & 1\\ \hfill 0\hfill & \hfill 0\hfill & 1\end{array}}$

The negation $\neg p$ is equivalent to p NAND p.

The disjunction $p\vee q$ is equivalent to $(p\mathrm{NAND}p)\mathrm{NAND}(q\mathrm{NAND}q)$.

Can you make up three circuits, using only the NAND gate, that are equivalent to the conjunction $\wedge$, to the conditional $\Rightarrow$ and to the bi-conditional $\iff$?

If you have worked through this article you should now be able to solve the problems Simple Counting Machine, Adding Machine and Circular Circuitry and not just by trial and error, and you should be able to explain the circuits.